Sylvester equation
Encyclopedia
The Sylvester equation, commonly encountered in control theory
, is the matrix
equation
of the form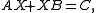
where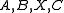
are 
matrices.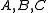 
are known. The problem is to find 
.
notation and the vectorization operator
, we can rewrite the equation in the form
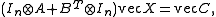
where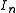
is the 
identity matrix
. In this form, the Sylvester equation can be seen as a linear system
of dimension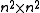
.
If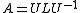
and 
are the Jordan canonical forms of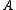 
and 
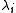, and 
and 
are their eigenvalues, one can write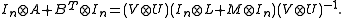
Since
is upper triangular
with diagonal elements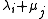
, the matrix on the left hand side is singular if and only if there exist 
and 
such that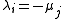 
.
Therefore, we have proved that the Sylvester equation has a unique solution if and only if
and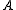 
have no common eigenvalues.
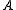and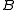 
into Schur form
by a QR algorithm
, and then solving the resulting triangular system via back-substitution
. This algorithm, whose computational cost is O
arithmetical operations, is used, among others, by LAPACK
and the
.
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, is the matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
of the form
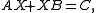
whe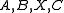re
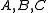are matrices. are known. The problem is to find .Existence and uniqueness of the solution
Using the Kronecker productKronecker product
In mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix...
notation and the vectorization operator
Vectorization (mathematics)
In mathematics, especially in linear algebra and matrix theory, the vectorization of a matrix is a linear transformation which converts the matrix into a column vector...
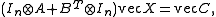
, we can rewrite the equation in the formwhere
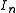is the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. In this form, the Sylvester equation can be seen as a linear system
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
of dimension
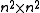.If
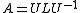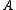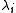and are the Jordan canonical forms of and , and and are their eigenvalues, one can write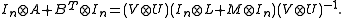Since
is upper triangularTriangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
with diagonal elements
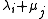, the matrix on the left hand side is singular if and only if there exist and such that 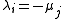.Therefore, we have proved that the Sylvester equation has a unique solution if and only if
and 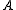have no common eigenvalues.Numerical solutions
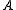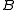A classical algorithm for the numerical solution of the Sylvester equation is the Bartels–Stewart algorithm, which consists of transforming and into Schur formSchur decomposition
In the mathematical discipline of linear algebra, the Schur decomposition or Schur triangulation, named after Issai Schur, is a matrix decomposition.- Statement :...
by a QR algorithm
QR algorithm
In numerical linear algebra, the QR algorithm is an eigenvalue algorithm: that is, a procedure to calculate the eigenvalues and eigenvectors of a matrix. The QR transformation was developed in the late 1950s by John G.F. Francis and by Vera N. Kublanovskaya , working independently...
, and then solving the resulting triangular system via back-substitution
Triangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
. This algorithm, whose computational cost is O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
arithmetical operations, is used, among others, by LAPACKLAPACK
-External links:* : a modern replacement for PLAPACK and ScaLAPACK* on Netlib.org* * * : a modern replacement for LAPACK that is MultiGPU ready* on Sourceforge.net* * optimized LAPACK for Solaris OS on SPARC/x86/x64 and Linux* * *...
and the
lyap function in GNU OctaveGNU Octave
GNU Octave is a high-level language, primarily intended for numerical computations. It provides a convenient command-line interface for solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with MATLAB...
.