Not to be confused with SimPy

SimPy

SimPy is a process-based, object-oriented discrete-event simulation language. It is implemented in standard Python and released as open source software under the GNU Lesser General Public License...

, a discrete-event simulation language.

SymPy is a Python library for symbolic computation

Symbolic computation

Symbolic computation or algebraic computation, relates to the use of machines, such as computers, to manipulate mathematical equations and expressions in symbolic form, as opposed to manipulating the approximations of specific numerical quantities represented by those symbols...

. The stated goals of the library are to become a full-featured computer algebra system

Computer algebra system

A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...

 and to keep a simple code base to promote extensibility

Extensibility

In software engineering, extensibility is a system design principle where the implementation takes into consideration future growth. It is a systemic measure of the ability to extend a system and the level of effort required to implement the extension...

 and comprehensibility. SymPy is written in Python.

SymPy is free software

Free software

Free software, software libre or libre software is software that can be used, studied, and modified without restriction, and which can be copied and redistributed in modified or unmodified form either without restriction, or with restrictions that only ensure that further recipients can also do...

. The lead developers are Ondřej Čertík and Aaron Meurer.

Features

The SymPy library is split into a core with many optional modules.

Currently, the core of SymPy has around 13,000 lines of code (including comments and docstring

Docstring

In programming, a docstring is a string literal specified in source code that is used, like a comment, to document a specific segment of code. Unlike conventional source code comments, or even specifically formatted comments like Javadoc documentation, docstrings are not stripped from the source...

s) and its capabilities include:

• basic arithmetics *, /, +, -, **
• basic simplification (like a*b*b + 2*b*a*b → 3*a*b**2)
• expansion (like (a+b)**2 → a**2 + 2*a*b + b**2)
• functions (exp, ln, ...)
• complex numbers (like exp(I*x).expand(complex=True) → cos(x)+I*sin(x))
• differentiation
  Derivative
  In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
  
  
• Taylor (Laurent) series
  Laurent series
  In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
  
  
• substitution (like x → ln(x), or sin → cos)
• arbitrary precision integers, rationals and floats
• noncommutative symbols
• pattern matching

The complete set of SymPy modules (which are 73,000 lines including documentation) are specialised for performing the following tasks:

• more functions (sin, cos, tan, atan, asin, acos, factorial, zeta, legendre)
• limits
  Limit (mathematics)
  In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
  
   (like limit(x*log(x), x, 0) → 0)
• integration
  Integral
  Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
  
   using extended Risch-Norman heuristic
• polynomials (division, gcd, square free decomposition, groebner bases, factorization)
• solvers (algebraic, difference and differential equations, and systems of equations)
• symbolic matrices (determinants, LU decomposition...)
• Pauli and Dirac algebra
• geometry module
• plotting (2D and 3D)

Sympy includes tools for applications in quantum physics, Fourier series

Fourier series

In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...

, differential geometry, and relativity

General relativity

General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...

.
There are also a set of self-tests (15,000 lines in 142 files) for most features in SymPy.

Related projects

• Sage: an open source alternative to Mathematica
  Mathematica
  Mathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...
  
  , Maple
  Maple (software)
  Maple is a general-purpose commercial computer algebra system. It was first developed in 1980 by the Symbolic Computation Group at the University of Waterloo in Waterloo, Ontario, Canada....
  
  , Matlab
  MATLAB
  MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
  
   and Magma
  Magma computer algebra system
  Magma is a computer algebra system designed to solve problems in algebra, number theory, geometry and combinatorics. It is named after the algebraic structure magma...
  
   (SymPy is included in Sage)
• mpmath: a Python library for arbitrary-precision floating-point arithmetic (included in SymPy)
• sympycore: another Python CAS
• symbide: GUI
  Gui
  Gui or guee is a generic term to refer to grilled dishes in Korean cuisine. These most commonly have meat or fish as their primary ingredient, but may in some cases also comprise grilled vegetables or other vegetarian ingredients. The term derives from the verb, "gupda" in Korean, which literally...
  
   for SymPy in PyGTK
  PyGTK
  PyGTK is a set of Python wrappers for the GTK+ graphical user interface library. PyGTK is free software and licensed under the LGPL. It is analogous to PyQt and wxPython which are python wrappers for Qt and wxWidgets respectively. Its original author is the prominent GNOME developer James Henstridge...
  
  
• symfe: Lightweight symbolic finite element calculations in Python

Pretty Printing

Sympy allows outputs to be formatted into a more appealing format through the pprint function. Alternatively, the init_printing method will enable pretty printing, so pprint need not be called. Pretty printing will use unicode symbols when available in the current environment, otherwise it will fall back to ASCII

ASCII

The American Standard Code for Information Interchange is a character-encoding scheme based on the ordering of the English alphabet. ASCII codes represent text in computers, communications equipment, and other devices that use text...

characters.

>>> from sympy import pprint, init_printing, Symbol, sin, cos, exp, sqrt, series, Integral, Function
>>>
>>> x = Symbol("x")
>>> y = Symbol("y")
>>> f = Function('f')
>>> # pprint will default to unicode if available
>>> pprint( x**exp(x) )
⎛ x⎞
⎝ℯ ⎠
x
>>> # An output without unicode
>>> pprint(Integral(f(x), x), use_unicode=False)
/
|
| f(x) dx
|
/
>>> # Compare with same expression but this time unicode is enabled
>>> pprint(Integral(f(x), x), use_unicode=True)
⌠
⎮ f(x) dx
⌡
>>> # Alternatively, you can call init_printing once and pretty print without the pprint function.
>>> init_printing
>>> sqrt(sqrt(exp(x)))
x
─
4
ℯ
>>> (1/cos(x)).series(x, 0, 10)
2 4 6 8
x 5⋅x 61⋅x 277⋅x ⎛ 10⎞
1 + ── + ──── + ───── + ────── + O⎝x ⎠
2 24 720 8064

Expansion

>>> from sympy import init_printing, Symbol, expand
>>> init_printing
>>>
>>> a = Symbol('a')
>>> b = Symbol('b')
>>> e = (a + b)**5
>>> e
5
(a + b)
>>> e.expand
5 4 3 2 2 3 4 5
a + 5⋅a ⋅b + 10⋅a ⋅b + 10⋅a ⋅b + 5⋅a⋅b + b

Arbitrary Precision Example

>>> from sympy import Rational, pprint
>>>
>>> e = Rational(2)**50 / Rational(10)**50
>>> pprint(e)
1/88817841970012523233890533447265625

Differentiation

>>> from sympy import init_printing, symbols, ln, diff
>>> init_printing
>>> x,y = symbols('x y')
>>> f = x**2 / y + 2 * x - ln(y)
>>> diff(f,x)
2⋅x
─── + 2
y
>>> diff(f,y)
2
x 1
- ── - ─
2 y
y
>>> diff(diff(f,x),y)
-2⋅x
────
2
y

Plotting

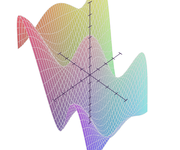
>>> from sympy import symbols, Plot, cos
>>> x,y = symbols('x y')
>>> Plot(cos(x*3)*cos(y*5)-y)
[0]: -y + cos(3*x)*cos(5*y), 'mode=cartesian'

Limits

>>> from sympy import init_printing, Symbol, limit, sqrt, oo
>>> init_printing
>>>
>>> x = Symbol('x')
>>> limit(sqrt(x**2 - 5*x + 6) - x, x, oo)
-5/2
>>> limit(x*(sqrt(x**2 + 1) - x), x, oo)
1/2
>>> limit(1/x**2, x, 0)
∞
>>> limit(((x - 1)/(x + 1))**x, x, oo)
-2
ℯ

Differential Equations

>>> from sympy import init_printing, Symbol, Function, Eq, dsolve, sin, diff
>>> init_printing
>>>
>>> x = Symbol("x")
>>> f = Function("f")
>>>
>>> eq = Eq(f(x).diff(x), f(x))
>>> eq
d
──(f(x)) = f(x)
dx
>>>
>>> dsolve(eq, f(x))
x
f(x) = C₁⋅ℯ

>>>
>>> eq = Eq(x**2*f(x).diff(x), -3*x*f(x) + sin(x)/x)
>>> eq
2 d sin(x)
x ⋅──(f(x)) = -3⋅x⋅f(x) + ──────
dx x
>>>
>>> dsolve(eq, f(x))
C₁ - cos(x)
f(x) = ───────────
3
x

Integration

>>> from sympy import init_printing, integrate, Symbol, exp, cos, erf
>>> init_printing
>>> x = Symbol('x')
>>> # Polynomial Function
>>> f = x**2 + x + 1
>>> f
2
x + x + 1
>>> integrate(f,x)
3 2
x x
── + ── + x
3 2
>>> # Rational Function
>>> f = x/(x**2+2*x+1)
>>> f
x
────────────
2
x + 2⋅x + 1

>>> integrate(f, x)
1
log(x + 1) + ─────
x + 1
>>> # Exponential-polynomial functions
>>> f = x**2 * exp(x) * cos(x)
>>> f
2 x
x ⋅ℯ ⋅cos(x)
>>> integrate(f, x)
2 x 2 x x x
x ⋅ℯ ⋅sin(x) x ⋅ℯ ⋅cos(x) x ℯ ⋅sin(x) ℯ ⋅cos(x)
──────────── + ──────────── - x⋅ℯ ⋅sin(x) + ───────── - ─────────
2 2 2 2
>>> # A non-elementary integral
>>> f = exp(-x**2) * erf(x)
>>> f
2
-x
ℯ ⋅erf(x)
>>> integrate(f, x)

___ 2
╲╱ π ⋅erf (x)
─────────────
4

Series

>>> from sympy import Symbol, cos, sin, pprint
>>> x = Symbol('x')
>>> e = 1/cos(x)
>>> pprint(e)
1
──────
cos(x)
>>> pprint(e.series(x, 0, 10))
2 4 6 8
x 5⋅x 61⋅x 277⋅x ⎛ 10⎞
1 + ── + ──── + ───── + ────── + O⎝x ⎠
2 24 720 8064
>>> e = 1/sin(x)
>>> pprint(e)
1
──────
sin(x)
>>> pprint(e.series(x, 0, 4))
3
1 x 7⋅x ⎛ 4⎞
─ + ─ + ──── + O⎝x ⎠
x 6 360

External links

• SymPy Project Home
• Planet SymPy
• Code Repository on Github