Symmetric design
Encyclopedia
In combinatorial
mathematics
, a symmetric design is a block design with equal numbers of points and blocks. Thus, it has the fewest possible blocks given the number of points (by Fisher's inequality
). They are also known as projective designs.
That is, a symmetric design is a (v,b,r,k,λ)-design with b = v and r = k. Either of the latter two equations implies the other. In fact, the parameters of a symmetric design satisfy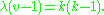
Clearly, this imposes strong restrictions on v, so the number of points is far from arbitrary. The Bruck–Ryser–Chowla theorem gives necessary but not sufficient conditions.
A theorem of Ryser gives a different combinatorial condition for an incidence structure
to be symmetric. If X is a v-element set (the "point set"), and B is a v-element class of k-element subsets (called "blocks"), and any two blocks have exactly λ points in common, then (X, B) is a symmetric design.
s (λ = 1) and biplane geometries (λ = 2).
The order of a symmetric design is defined to be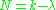
; For example, an order N projective plane has 
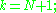the terminology is because the projective plane over a field of q elements has lines with 
points.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a symmetric design is a block design with equal numbers of points and blocks. Thus, it has the fewest possible blocks given the number of points (by Fisher's inequality
Fisher's inequality
In combinatorial mathematics, Fisher's inequality, named after Ronald Fisher, is a necessary condition for the existence of a balanced incomplete block design satisfying certain prescribed conditions....
). They are also known as projective designs.
That is, a symmetric design is a (v,b,r,k,λ)-design with b = v and r = k. Either of the latter two equations implies the other. In fact, the parameters of a symmetric design satisfy
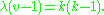
Clearly, this imposes strong restrictions on v, so the number of points is far from arbitrary. The Bruck–Ryser–Chowla theorem gives necessary but not sufficient conditions.
A theorem of Ryser gives a different combinatorial condition for an incidence structure
Incidence structure
In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
to be symmetric. If X is a v-element set (the "point set"), and B is a v-element class of k-element subsets (called "blocks"), and any two blocks have exactly λ points in common, then (X, B) is a symmetric design.
Examples
Examples include finite projective planeProjective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
s (λ = 1) and biplane geometries (λ = 2).
The order of a symmetric design is defined to be
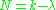; For example, an order N projective plane has 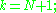the terminology is because the projective plane over a field of q elements has lines with points.See also
- Association schemeAssociation schemeThe theory of association schemes arose in statistics, in the theory of experimental design for the analysis of variance. In mathematics, association schemes belong to both algebra and combinatorics. Indeed, in algebraic combinatorics, association schemes provide a unified approach to many topics,...
- Block design
- Combinatorial designCombinatorial designCombinatorial design theory is the part of combinatorial mathematics that deals with the existence and construction of systems of finite sets whose intersections have specified numerical properties....
- Design of experimentsDesign of experimentsIn general usage, design of experiments or experimental design is the design of any information-gathering exercises where variation is present, whether under the full control of the experimenter or not. However, in statistics, these terms are usually used for controlled experiments...
- Variance analysisAnalysis of varianceIn statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
External links
- Design DB: A database of combinatorial, statistical, experimental block designs