Syncategorematic term
Encyclopedia
In scholastic logic, a syncategorematic term (syncategoremata) is a word that cannot serve as the subject or the predicate of a proposition, and thus cannot stand for any of Aristotle's categories, but can be used with other terms to form a proposition. Words such as 'all', 'and', 'if' are examples of such terms.
The distinction between categorematic and syncategorematic terms was established in ancient Greek grammar. Words that designate self-sufficient entities (i.e., nouns or adjectives) were called categorematic, and those that do not stand by themselves were dubbed syncategorematic, (i.e., prepositions, logical connectives, etc.). Priscian
in his Institutiones grammaticae translates the word as consignificantia. Scholastics retained the difference, which became a dissertable topic after the 13th century revival of logic. William of Sherwood
, a representative of terminism, wrote a treatise called Syncategoremata. Later his pupil, Peter of Spain
, produced a similar work entitled Syncategoreumata.
In propositional calculus
, a syncategorematic term is a term that has no individual meaning (a term with an individual meaning is called categorematic). Whether a term is syncategorematic or not is determined by the way it is defined or introduced in the language.
In the common definition of propositional logic, examples of syncategorematic terms are the logical connectives. Let us take the connective
for instance, its semantic rule is:
iff 
So its meaning is defined when it occurs in combination with two formulas
and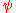 
. But is has no meaning when taken in isolation, i.e. 
is not defined.
We could however define the
in a different manner, e.g., using λ-abstraction
:
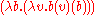which expects a pair of Boolean-valued arguments, i.e., arguments which are either TRUE or FALSE, defined as 
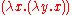and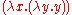 
respectively. This is an expression of type
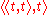. Its meaning is thus a binary function from pairs of entities of type truth-value to an entity of type truth-value. Under this definition it would be non-syncategorematic, or categorematic. Note that while this definition would formally define the 
function, it requires the use of 
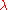-abstraction, in which case the 
itself is introduced syncategorematically, thus simply moving the issue up another level of abstraction.
The distinction between categorematic and syncategorematic terms was established in ancient Greek grammar. Words that designate self-sufficient entities (i.e., nouns or adjectives) were called categorematic, and those that do not stand by themselves were dubbed syncategorematic, (i.e., prepositions, logical connectives, etc.). Priscian
Priscian
Priscianus Caesariensis , commonly known as Priscian, was a Latin grammarian. He wrote the Institutiones grammaticae on the subject...
in his Institutiones grammaticae translates the word as consignificantia. Scholastics retained the difference, which became a dissertable topic after the 13th century revival of logic. William of Sherwood
William of Sherwood
William of Sherwood was a medieval English Scholastic philosopher, logician and teacher.Little is known of his life, but he is thought to have studied in Paris, as a master at Oxford in 1252, treasurer of Lincoln from 1254/8 onwards, and a rector of Aylesbury.He was the author of two books which...
, a representative of terminism, wrote a treatise called Syncategoremata. Later his pupil, Peter of Spain
Peter of Spain
Peter of Spain or, in Latin, Petrus Hispanus is the Mediaeval author of Tractatus, later known as Summulae logicales magistri Petri Hispani , a standard textbook on logic...
, produced a similar work entitled Syncategoreumata.
In propositional calculus
Propositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
, a syncategorematic term is a term that has no individual meaning (a term with an individual meaning is called categorematic). Whether a term is syncategorematic or not is determined by the way it is defined or introduced in the language.
In the common definition of propositional logic, examples of syncategorematic terms are the logical connectives. Let us take the connective
for instance, its semantic rule is: iff So its meaning is defined when it occurs in combination with two formulas
and 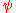. But is has no meaning when taken in isolation, i.e. is not defined.We could however define the
in a different manner, e.g., using λ-abstractionLambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
:
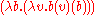which expects a pair of Boolean-valued arguments, i.e., arguments which are either TRUE or FALSE, defined as 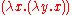and 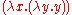respectively. This is an expression of typeType system
A type system associates a type with each computed value. By examining the flow of these values, a type system attempts to ensure or prove that no type errors can occur...
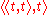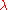. Its meaning is thus a binary function from pairs of entities of type truth-value to an entity of type truth-value. Under this definition it would be non-syncategorematic, or categorematic. Note that while this definition would formally define the function, it requires the use of -abstraction, in which case the itself is introduced syncategorematically, thus simply moving the issue up another level of abstraction.