Sz.-Nagy's dilation theorem
Encyclopedia
The Sz.-Nagy dilation theorem (proved by Béla Szőkefalvi-Nagy
) states that every contraction T on a Hilbert space
H has a unitary dilation U to a Hilbert space K, containing H, with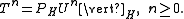
Moreover, such a dilation is unique (up to unitary equivalence) when one assumes K is minimal, in the sense that the linear span of ∪nUnK is dense in K. When this minimality condition holds, U is called the minimal unitary dilation of T.
T (i.e., (
), its defect operator DT is defined to be the (unique) positive square root DT = (I - T*T)½. In the special case that S is an isometry, the following is an Sz. Nagy unitary dilation of S with the required polynomial functional calculus property:
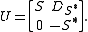
Also, every contraction T on a Hilbert space H has an isometric dilation, again with the calculus property, on
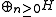
given by
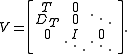
Applying the above two constructions successively gives a unitary dilation for a contraction T:
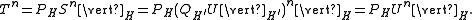
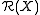
is a Dirichlet algebra
, then T has a minimal normal δX dilation, of the form above. A consequence of this is that any operator with a simply connected spectral set X has a minimal normal δX dilation.
To see that this generalises Sz.-Nagy's theorem, note that contraction operators have the unit disc D as a spectral set, and that normal operators with spectrum in the unit circle δD are unitary.
Bela Szokefalvi-Nagy
Béla Szőkefalvi-Nagy was a Hungarian mathematician. His father, Gyula Szőkefalvi-Nagy was also a famed mathematician. Szőkefalvi-Nagy collaborated with Alfréd Haar and Frigyes Riesz, founders of the Szegedian school of mathematics. He contributed to the theory of Fourier series and approximation...
) states that every contraction T on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H has a unitary dilation U to a Hilbert space K, containing H, with
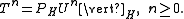
Moreover, such a dilation is unique (up to unitary equivalence) when one assumes K is minimal, in the sense that the linear span of ∪nUnK is dense in K. When this minimality condition holds, U is called the minimal unitary dilation of T.
Proof
For a contractionContraction (operator theory)
In operator theory, a bounded operator T: X → Y between normed vector spaces X and Y is said to be a contraction if its operator norm ||T|| ≤ 1. Every bounded operator becomes a contraction after suitable scaling...
T (i.e., (
), its defect operator DT is defined to be the (unique) positive square root DT = (I - T*T)½. In the special case that S is an isometry, the following is an Sz. Nagy unitary dilation of S with the required polynomial functional calculus property: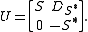Also, every contraction T on a Hilbert space H has an isometric dilation, again with the calculus property, on
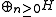
given by
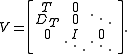
Applying the above two constructions successively gives a unitary dilation for a contraction T:
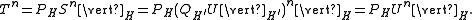
Schaffer form
The Schaffer form of a unitary Sz. Nagy dilation can be viewed as a beginning point for the characterization of all unitary dilations, with the required property, for a given contraction.Remarks
A generalisation of this theorem, by Berger, Foias and Lebow, shows that if X is a spectral set for T, and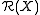is a Dirichlet algebra
Dirichlet algebra
In mathematics, a Dirichlet algebra is a particular type of algebra associated to a compact Hausdorff space X. It is a closed subalgebra of C, the uniform algebra of bounded continuous functions on X, whose real parts are dense in the algebra of bounded continuous real functions on X...
, then T has a minimal normal δX dilation, of the form above. A consequence of this is that any operator with a simply connected spectral set X has a minimal normal δX dilation.
To see that this generalises Sz.-Nagy's theorem, note that contraction operators have the unit disc D as a spectral set, and that normal operators with spectrum in the unit circle δD are unitary.