Contraction (operator theory)
Encyclopedia
In operator theory
, a bounded operator
T: X → Y between normed vector space
s X and Y is said to be a contraction if its operator norm
||T|| ≤ 1. Every bounded operator becomes a contraction after suitable scaling. The analysis of contractions provides insight into the structure of operators, or a family of operators.
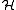. We define some basic objects associated with T.
The defect operators of T are the operators DT = (1 − T*T)½ and DT* = (1 − TT*)½. The square root is the positive semidefinite one
given by the spectral theorem
. The defect spaces
and 
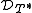are the ranges Ran(DT) and Ran(DT*) respectively. The positive operator DT induces an inner product on 
. The space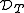 
can be identified naturally with 
, with the induced inner product. The same can be said for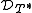 
.
The defect indices of T are the pair
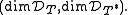
The defect operators and the defect indices are a measure of the non-unitarity of T.
A contraction T on a Hilbert space can be canonically decomposed into an orthogonal direct sum
where U is a unitary operator and Γ is completely non-unitary in the sense that it has no reducing subspaces on which its restriction is unitary. If U = 0, T is said to be a completely non-unitary contraction. A special case of this decomposition is the Wold decomposition
for an isometry
, where Γ is a proper isometry.
Contractions on Hilbert spaces can be viewed as the operator analogs of cos θ and are called operator angles in some contexts. The explicit description of contractions leads to (operator-)parametrizations of positive and unitary matrices.
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, a bounded operator
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
T: X → Y between normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
s X and Y is said to be a contraction if its operator norm
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
||T|| ≤ 1. Every bounded operator becomes a contraction after suitable scaling. The analysis of contractions provides insight into the structure of operators, or a family of operators.
Contractions on a Hilbert space
Consider the special case where T is a contraction acting on a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
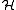. We define some basic objects associated with T.The defect operators of T are the operators DT = (1 − T*T)½ and DT* = (1 − TT*)½. The square root is the positive semidefinite one
Square root of a matrix
In mathematics, the square root of a matrix extends the notion of square root from numbers to matrices. A matrix B is said to be a square root of A if the matrix product B · B is equal to A.-Properties:...
given by the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
. The defect spaces
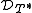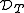and are the ranges Ran(DT) and Ran(DT*) respectively. The positive operator DT induces an inner product on . The space can be identified naturally with , with the induced inner product. The same can be said for 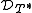.The defect indices of T are the pair
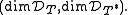
The defect operators and the defect indices are a measure of the non-unitarity of T.
A contraction T on a Hilbert space can be canonically decomposed into an orthogonal direct sum
where U is a unitary operator and Γ is completely non-unitary in the sense that it has no reducing subspaces on which its restriction is unitary. If U = 0, T is said to be a completely non-unitary contraction. A special case of this decomposition is the Wold decomposition
Wold decomposition
In operator theory, the Wold decomposition, named after Herman Wold, or Wold-von Neumann decomposition, after Wold and John von Neumann, is a classification theorem for isometric linear operators on a given Hilbert space...
for an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
, where Γ is a proper isometry.
Contractions on Hilbert spaces can be viewed as the operator analogs of cos θ and are called operator angles in some contexts. The explicit description of contractions leads to (operator-)parametrizations of positive and unitary matrices.