
Square root of a matrix
Encyclopedia
In mathematics
, the square root of a matrix extends the notion of square root
from numbers to matrices
. A matrix B is said to be a square root of A if the matrix product B · B is equal to A.
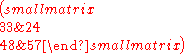
has square roots

and
 ,
,
as well as their additive inverse
s. Another example is the 2×2 identity matrix
 which has an infinitude of symmetric rational square roots given by
which has an infinitude of symmetric rational square roots given by 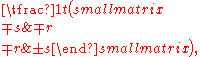
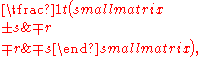
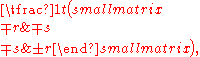
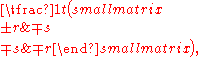
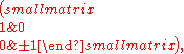 and
and  where (r, s, t) is any Pythagorean triple
where (r, s, t) is any Pythagorean triple
— that is, any set of positive integers such that
However, a positive-definite matrix
has precisely one positive-definite square root, which can be called its principal square root.
While the square root of an integer
is either again an integer or an irrational number
, in contrast an integer matrix can have a square root whose entries are rational, yet not integral. For example, the matrix

has a square root
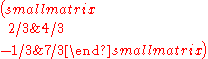 ,
,
as well as a square root that is an integer matrix:
 .
.
The other two square roots are the additive inverses of these (In general, a 2×2 matrix with two distinct eigenvalues has four square roots). The 2×2 identity matrix discussed above provides another example.
Just as with the real numbers, a real matrix may fail to have a real square root, but have a square root with complex
-valued entries.
that give up to four square roots, if the matrix has any roots.
If D is a diagonal
n × n matrix, one can obtain a square root by taking a diagonal matrix R, where each element along the diagonal is a square root of the corresponding element of D. If the diagonal elements of D are real and non-negative, and the square roots are taken with non-negative sign, the matrix R will be the principal root of D.
if there is a matrix V and a diagonal matrix D such that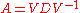 . This happens if and only if A has n eigenvectors which constitute a basis for Cn. In this case, V can be chosen to be the matrix with the n eigenvectors as columns, and a square root of
. This happens if and only if A has n eigenvectors which constitute a basis for Cn. In this case, V can be chosen to be the matrix with the n eigenvectors as columns, and a square root of  is
is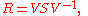
where S is any square root of D. Indeed,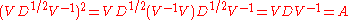
For example, the matrix

can be diagonalized as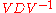 ,
,
where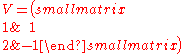 and
and
 .
.
 has principal square root
has principal square root 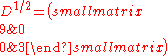 , giving the square root
, giving the square root 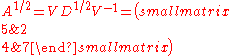 .
.
followed by a series expansion, similar to the approach described in logarithm of a matrix
.
. The iteration is defined by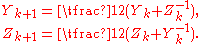
Convergence is not guaranteed, even for matrices that do have square roots, but if the process converges, the matrix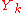 converges quadratically to a square root A1/2, while
converges quadratically to a square root A1/2, while 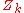 converges to its inverse, A−1/2. .
converges to its inverse, A−1/2. .
. The iteration is defined by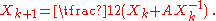
Again, convergence is not guaranteed, but if the process converges, the matrix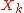 converges quadratically to a square root A1/2. Compared to Denman–Beavers iteration, an advantage of the Babylonian method is that only one matrix inverse need be computed per iteration step. However, unlike Denman–Beavers iteration, this method is numerically unstable and more likely to fail to converge.
converges quadratically to a square root A1/2. Compared to Denman–Beavers iteration, an advantage of the Babylonian method is that only one matrix inverse need be computed per iteration step. However, unlike Denman–Beavers iteration, this method is numerically unstable and more likely to fail to converge.
and operator theory
, given a bounded
positive semidefinite operator (a non-negative operator) T on a complex Hilbert space, B is a square root of T if T = B* B, where B* denotes the Hermitian adjoint
of B. According to the spectral theorem
, the continuous functional calculus
can be applied to obtain an operator T½ such that
T½ is itself positive and (T½)2 = T. The operator T½ is the unique non-negative square root of T.
A bounded non-negative operator on a complex Hilbert space is self adjoint by definition. So T = (T½)* T½. Conversely, it is trivially true that every operator of the form B* B is non-negative. Therefore, an operator T is non-negative if and only if
T = B* B for some B (equivalently, T = CC* for some C).
The Cholesky factorization provides another particular example of square root, which should not be confused with the unique non-negative square root.
Indeed, take B = T½ to be the unique non-negative square root of T. If T is strictly positive, then B is invertible, and so is unitary: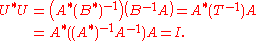
If T is non-negative without being strictly positive, then the inverse of B cannot be defined, but the Moore–Penrose pseudoinverse B+ can be. In that case, the operator is a partial isometry
, that is, a unitary operator from the range of T to itself. This can then be extended to a unitary operator U on the whole space by setting it equal to the identity on the kernel of T. More generally, this is true on an infinite-dimensional Hilbert space if, in addition, T has closed range
. In general, if A, B are closed and densely defined operators
on a Hilbert space H, and A* A = B* B, then A = UB where U is a partial isometry.
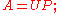
this is the polar decomposition of A. The positive operator P is the unique positive square root of the positive operator A∗A, and U is defined by .
If A is not invertible, then it still has a polar composition in which P is defined in the same way (and is unique). The unitary operator U is not unique. Rather it is possible to determine a "natural" unitary operator as follows: AP+ is a unitary operator from the range of A to itself, which can be extended by the identity on the kernel of A∗. The resulting unitary operator U then yields the polar decomposition of A.
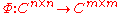
is completely positive if and only if it is of the form

where k ≤ nm. Let {Ep q} ⊂ Cn × n be the n2 elementary matrix units. The positive matrix
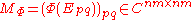
is called the Choi matrix of Φ. The Kraus operators correspond to the, not necessarily square, square roots of MΦ: For any square root B of MΦ, one can obtain a family of Kraus operators Vi by undoing the Vec operation to each column bi of B. Thus all sets of Kraus operators are related by partial isometries.
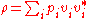
where ∑ pi = 1, the set
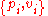
is said to be an ensemble that describes the mixed state ρ. Notice {vi} is not required to be orthogonal. Different ensembles describing the state ρ are related by unitary operators, via the square roots of ρ. For instance, suppose
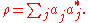
The trace 1 condition means
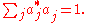
Let

and vi be the normalized ai. We see that
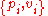
gives the mixed state ρ.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the square root of a matrix extends the notion of square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
from numbers to matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. A matrix B is said to be a square root of A if the matrix product B · B is equal to A.
Properties
In general, a matrix can have many square roots. For example, the matrix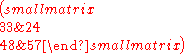
has square roots

and
 ,
,as well as their additive inverse
Additive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
s. Another example is the 2×2 identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
 which has an infinitude of symmetric rational square roots given by
which has an infinitude of symmetric rational square roots given by 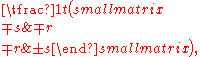
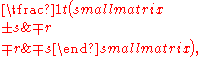
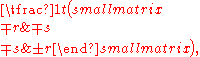
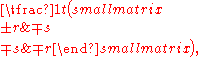
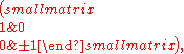 and
and  where (r, s, t) is any Pythagorean triple
where (r, s, t) is any Pythagorean triplePythagorean triple
A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
— that is, any set of positive integers such that

However, a positive-definite matrix
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
has precisely one positive-definite square root, which can be called its principal square root.
While the square root of an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
is either again an integer or an irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
, in contrast an integer matrix can have a square root whose entries are rational, yet not integral. For example, the matrix

has a square root
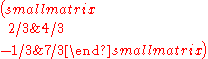 ,
,as well as a square root that is an integer matrix:
 .
.The other two square roots are the additive inverses of these (In general, a 2×2 matrix with two distinct eigenvalues has four square roots). The 2×2 identity matrix discussed above provides another example.
Just as with the real numbers, a real matrix may fail to have a real square root, but have a square root with complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued entries.
Explicit formulas
For a 2 × 2 matrix, there are explicit formulasSquare root of a 2 by 2 matrix
A square root of a 2 by 2 matrix M is another 2 by 2 matrix R such that M = R2, where R2 stands for the matrix product of R with itself...
that give up to four square roots, if the matrix has any roots.
If D is a diagonal
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
n × n matrix, one can obtain a square root by taking a diagonal matrix R, where each element along the diagonal is a square root of the corresponding element of D. If the diagonal elements of D are real and non-negative, and the square roots are taken with non-negative sign, the matrix R will be the principal root of D.
By diagonalization
An n × n matrix A is diagonalizableDiagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
if there is a matrix V and a diagonal matrix D such that
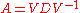 . This happens if and only if A has n eigenvectors which constitute a basis for Cn. In this case, V can be chosen to be the matrix with the n eigenvectors as columns, and a square root of
. This happens if and only if A has n eigenvectors which constitute a basis for Cn. In this case, V can be chosen to be the matrix with the n eigenvectors as columns, and a square root of  is
is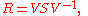
where S is any square root of D. Indeed,
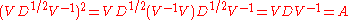
For example, the matrix

can be diagonalized as
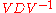 ,
,where
 and
and .
. has principal square root
has principal square root 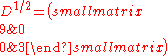 , giving the square root
, giving the square root 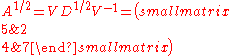 .
.By Jordan decomposition
For non-diagonalizable matrices one can calculate the Jordan normal formJordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
followed by a series expansion, similar to the approach described in logarithm of a matrix
Logarithm of a matrix
In mathematics, a logarithm of a matrix is another matrix such that the matrix exponential of the latter matrix equals the original matrix. It is thus a generalization of the scalar logarithm and in some sense an inverse function of the matrix exponential. Not all matrices have a logarithm and...
.
By Denman–Beavers iteration
Another way to find the square root of an n × n matrix A is the Denman–Beavers square root iteration. Let Y0 = A and Z0 = I, where I is the n × n identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. The iteration is defined by
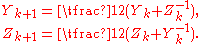
Convergence is not guaranteed, even for matrices that do have square roots, but if the process converges, the matrix
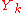 converges quadratically to a square root A1/2, while
converges quadratically to a square root A1/2, while 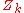 converges to its inverse, A−1/2. .
converges to its inverse, A−1/2. .By the Babylonian method
Yet another iterative method is obtained by taking the well-known formula of the Babylonian method for computing the square root of a real number, and applying it to matrices. Let X0 = I, where I is the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. The iteration is defined by
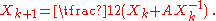
Again, convergence is not guaranteed, but if the process converges, the matrix
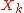 converges quadratically to a square root A1/2. Compared to Denman–Beavers iteration, an advantage of the Babylonian method is that only one matrix inverse need be computed per iteration step. However, unlike Denman–Beavers iteration, this method is numerically unstable and more likely to fail to converge.
converges quadratically to a square root A1/2. Compared to Denman–Beavers iteration, an advantage of the Babylonian method is that only one matrix inverse need be computed per iteration step. However, unlike Denman–Beavers iteration, this method is numerically unstable and more likely to fail to converge.Square roots of positive operators
In linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
and operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, given a bounded
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
positive semidefinite operator (a non-negative operator) T on a complex Hilbert space, B is a square root of T if T = B* B, where B* denotes the Hermitian adjoint
Hermitian adjoint
In mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
of B. According to the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
, the continuous functional calculus
Continuous functional calculus
In mathematics, the continuous functional calculus of operator theory and C*-algebra theory allows applications of continuous functions to normal elements of a C*-algebra. More precisely,Theorem...
can be applied to obtain an operator T½ such that
T½ is itself positive and (T½)2 = T. The operator T½ is the unique non-negative square root of T.
A bounded non-negative operator on a complex Hilbert space is self adjoint by definition. So T = (T½)* T½. Conversely, it is trivially true that every operator of the form B* B is non-negative. Therefore, an operator T is non-negative if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
T = B* B for some B (equivalently, T = CC* for some C).
The Cholesky factorization provides another particular example of square root, which should not be confused with the unique non-negative square root.
Unitary freedom of square roots
If T is a non-negative operator on a finite dimensional Hilbert space, then all square roots of T are related by unitary transformations. More precisely, if T = AA* = BB*, then there exists a unitary U s.t. A = BU.Indeed, take B = T½ to be the unique non-negative square root of T. If T is strictly positive, then B is invertible, and so is unitary:
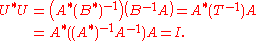
If T is non-negative without being strictly positive, then the inverse of B cannot be defined, but the Moore–Penrose pseudoinverse B+ can be. In that case, the operator is a partial isometry
Partial isometry
In functional analysis a partial isometry is a linear map W between Hilbert spaces H and K such that the restriction of W to the orthogonal complement of its kernel is an isometry...
, that is, a unitary operator from the range of T to itself. This can then be extended to a unitary operator U on the whole space by setting it equal to the identity on the kernel of T. More generally, this is true on an infinite-dimensional Hilbert space if, in addition, T has closed range
Closed range theorem
In the mathematical theory of Banach spaces, the closed range theorem gives necessary and sufficient conditions for a closed densely defined operator to have closed range...
. In general, if A, B are closed and densely defined operators
Unbounded operator
In mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....
on a Hilbert space H, and A* A = B* B, then A = UB where U is a partial isometry.
Some applications
Square roots, and the unitary freedom of square roots have applications throughout functional analysis and linear algebra.Polar decomposition
If A is an invertible operator on a finite-dimensional Hilbert space, then there is a unique unitary operator U and positive operator P such that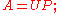
this is the polar decomposition of A. The positive operator P is the unique positive square root of the positive operator A∗A, and U is defined by .
If A is not invertible, then it still has a polar composition in which P is defined in the same way (and is unique). The unitary operator U is not unique. Rather it is possible to determine a "natural" unitary operator as follows: AP+ is a unitary operator from the range of A to itself, which can be extended by the identity on the kernel of A∗. The resulting unitary operator U then yields the polar decomposition of A.
Kraus operators
By Choi's result, a linear map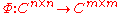
is completely positive if and only if it is of the form

where k ≤ nm. Let {Ep q} ⊂ Cn × n be the n2 elementary matrix units. The positive matrix
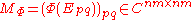
is called the Choi matrix of Φ. The Kraus operators correspond to the, not necessarily square, square roots of MΦ: For any square root B of MΦ, one can obtain a family of Kraus operators Vi by undoing the Vec operation to each column bi of B. Thus all sets of Kraus operators are related by partial isometries.
Mixed ensembles
In quantum physics, a density matrix for an n-level quantum system is an n × n complex matrix ρ that is positive semidefinite with trace 1. If ρ can be expressed as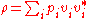
where ∑ pi = 1, the set
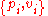
is said to be an ensemble that describes the mixed state ρ. Notice {vi} is not required to be orthogonal. Different ensembles describing the state ρ are related by unitary operators, via the square roots of ρ. For instance, suppose
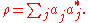
The trace 1 condition means
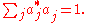
Let

and vi be the normalized ai. We see that
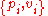
gives the mixed state ρ.

