
Square root of a 2 by 2 matrix
Encyclopedia
A square root
of a 2 by 2 matrix
M is another 2 by 2 matrix R such that M = R2, where R2 stands for the matrix product of R with itself. In many cases, such a matrix R can be obtained by an explicit formula.
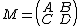
where A, B, C, and D may be real or complex numbers. Furthermore, let τ = A + D be the trace of M, and δ = AD - BC be its determinant
. Let s be such that s2 = δ, and t be such that t2 = τ + 2s. That is,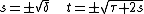
Then, if t ≠ 0, a square root of M is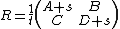
Indeed, the square of R is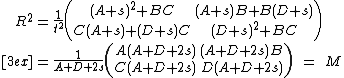
Note that R may have complex entries even if M is a real matrix; this will be the case, in particular, if the determinant δ is negative.
The general formula above fails completely if δ and τ are both zero; that is, if D = −A and A2 = −BC. In this case, if M is the null matrix (with A = B = C = D = 0), then the null matrix is also a square root of M; othwerwise M has no square root.
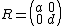
where a = ±√A and d = ±√D; which, depending on the sign choices, gives four, two, or one distinct matrices, if none of, only one of, or both A and D are zero, respectively.
If B is zero but A and D are not both zero, one can use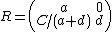
This formula will provide two solutions if A = D, and four otherwise. A similar formula can be used when C is zero but A and D are not both zero.
Square root of a matrix
In mathematics, the square root of a matrix extends the notion of square root from numbers to matrices. A matrix B is said to be a square root of A if the matrix product B · B is equal to A.-Properties:...
of a 2 by 2 matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
M is another 2 by 2 matrix R such that M = R2, where R2 stands for the matrix product of R with itself. In many cases, such a matrix R can be obtained by an explicit formula.
The general formula
Let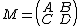
where A, B, C, and D may be real or complex numbers. Furthermore, let τ = A + D be the trace of M, and δ = AD - BC be its determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
. Let s be such that s2 = δ, and t be such that t2 = τ + 2s. That is,
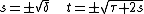
Then, if t ≠ 0, a square root of M is
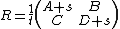
Indeed, the square of R is
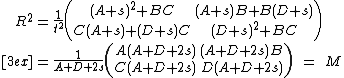
Note that R may have complex entries even if M is a real matrix; this will be the case, in particular, if the determinant δ is negative.
Special cases of the formula
In general, the formula above will provide four distinct square roots R, one for each choice of signs for s and t. If the determinant δ is zero but the trace τ is nonzero, the formula will give only two distinct solutions. Ditto if δ is nonzero and τ2 = 4δ, in which case one of the choices for s will make the denominator t be zero.The general formula above fails completely if δ and τ are both zero; that is, if D = −A and A2 = −BC. In this case, if M is the null matrix (with A = B = C = D = 0), then the null matrix is also a square root of M; othwerwise M has no square root.
Simplified formulas for special matrices
If M is diagonal (that is, B = C = 0), one can use the simplified formula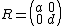
where a = ±√A and d = ±√D; which, depending on the sign choices, gives four, two, or one distinct matrices, if none of, only one of, or both A and D are zero, respectively.
If B is zero but A and D are not both zero, one can use
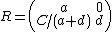
This formula will provide two solutions if A = D, and four otherwise. A similar formula can be used when C is zero but A and D are not both zero.

