
Table of costs of operations in elliptic curves
Encyclopedia
This table relates to the computational cost for certain operations used in elliptic curve cryptography
, used in practice for strong cryptographic security of a public key system. The columns of the table are labelled by various computational steps. The rows of the table are for different models of elliptic curve
s.
The table below contains the time-cost for these operations:
and the elliptic curve method of factorization (ECM
) it is necessary to consider the scalar multiplication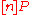 . So, one way to do this is to compute successively:
. So, one way to do this is to compute successively:
But, it is faster to use double-and-add method
,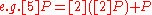 .
.
In general to compute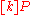 ,write
,write
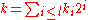
with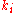 in {0,1} and
in {0,1} and 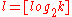 ,
,  , then:
, then:
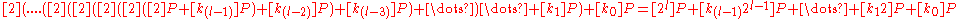 .
.
Note that, this simple algorithm takes at most 2l steps and each step consists of a doubling and (if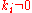 ) adding two points. So, this is one of the reasons why addition and doubling formulas are defined.
) adding two points. So, this is one of the reasons why addition and doubling formulas are defined.
Furthermore, this method is applicable to any group and if the group law is written multiplicatively, the double-and-add algorithm is instead called square-and-multiply algorithm
.
For more information about other possible operations on elliptic curves see http://hyperelliptic.org/EFD/g1p/index.html.
To see what adding (ADD) and doubling (DBL) points on elliptic curves mean, see The group law.
These are the operations considered in the table below:
DBL - Doubling
ADD - Addition
mADD - Mixed addition: addition of an input that has been scaled to have Z-coordinate 1.
mDBL - Mixed doubling: doubling of an input that has been scaled to have Z coordinate 1.
TPL - Tripling.
, the time-cost of these operations varies.
In this table it is assumed that:
This means that 100 multiplications (M) are required to invert (I) an element; 1 multiplication is required to compute the square (S) of an element; no multiplication is needed to multiply an element by a parameter (*param), by a constant (*const), nor to add two elements.
For more information about other results obtained with different assumptions, see http://hyperelliptic.org/EFD/g1p/index.html
Elliptic curve cryptography
Elliptic curve cryptography is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S...
, used in practice for strong cryptographic security of a public key system. The columns of the table are labelled by various computational steps. The rows of the table are for different models of elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s.
The table below contains the time-cost for these operations:
Abbreviations for the operations
In the next section a table of all the costs of some of the possible operations in elliptic curves is given. In some applications of elliptic curve cryptographyElliptic curve cryptography
Elliptic curve cryptography is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S...
and the elliptic curve method of factorization (ECM
Lenstra elliptic curve factorization
The Lenstra elliptic curve factorization or the elliptic curve factorization method is a fast, sub-exponential running time algorithm for integer factorization which employs elliptic curves. For general purpose factoring, ECM is the third-fastest known factoring method...
) it is necessary to consider the scalar multiplication
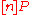 . So, one way to do this is to compute successively:
. So, one way to do this is to compute successively:But, it is faster to use double-and-add method
Exponentiation by squaring
Exponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add...
,
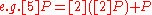 .
.In general to compute
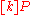 ,write
,write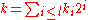
with
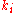 in {0,1} and
in {0,1} and 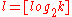 ,
,  , then:
, then: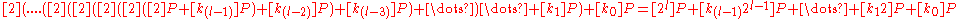 .
.Note that, this simple algorithm takes at most 2l steps and each step consists of a doubling and (if
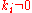 ) adding two points. So, this is one of the reasons why addition and doubling formulas are defined.
) adding two points. So, this is one of the reasons why addition and doubling formulas are defined.Furthermore, this method is applicable to any group and if the group law is written multiplicatively, the double-and-add algorithm is instead called square-and-multiply algorithm
Exponentiation by squaring
Exponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add...
.
For more information about other possible operations on elliptic curves see http://hyperelliptic.org/EFD/g1p/index.html.
To see what adding (ADD) and doubling (DBL) points on elliptic curves mean, see The group law.
These are the operations considered in the table below:
DBL - Doubling
ADD - Addition
mADD - Mixed addition: addition of an input that has been scaled to have Z-coordinate 1.
mDBL - Mixed doubling: doubling of an input that has been scaled to have Z coordinate 1.
TPL - Tripling.
Tabulation
Under different assumptions on the multiplication, addition, inversion for the elements in some fixed fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, the time-cost of these operations varies.
In this table it is assumed that:
- I = 100M, S = 1M, *param = 0M, add = 0M, *const = 0M
This means that 100 multiplications (M) are required to invert (I) an element; 1 multiplication is required to compute the square (S) of an element; no multiplication is needed to multiply an element by a parameter (*param), by a constant (*const), nor to add two elements.
For more information about other results obtained with different assumptions, see http://hyperelliptic.org/EFD/g1p/index.html
| Curve shape, representation | DBL | ADD | mADD | mDBL | TPL |
|---|---|---|---|---|---|
| Short Weierstrass projective Elliptic curve In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity... |
11 | 14 | 11 | 8 | |
| Short Weierstrass projective with a4=-1 Elliptic curve In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity... |
11 | 14 | 11 | 8 | |
| Short Weierstrass projective with a4=-3 Elliptic curve In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity... |
10 | 14 | 11 | 8 | |
| Tripling-oriented Doche–Icart–Kohel curve Tripling-oriented Doche–Icart–Kohel curve The tripling-oriented Doche–Icart–Kohel curve is a form of an elliptic curve that has been used lately in cryptography; it is a particular type of Weierstrass curve... |
9 | 17 | 11 | 6 | 12 |
| Hessian curve extended | 9 | 12 | 11 | 9 | |
| Hessian curve projective | 8 | 12 | 10 | 6 | 14 |
| Jacobi quartic XYZ | 8 | 13 | 11 | 5 | |
| Jacobi quartic doubling-oriented XYZ | 8 | 13 | 11 | 5 | |
| Twisted Hessian curve projective Twisted Hessian curves In mathematics, the Twisted Hessian curve represents a generalization of Hessian curves; it was introduced in elliptic curve cryptography to speed up the addition and doubling formulas and to have strongly unified arithmetic. In some operations , it is close in speed to Edwards... |
8 | 12 | 12 | 8 | 14 |
| Doubling-oriented Doche–Icart–Kohel curve Doubling-oriented Doche–Icart–Kohel curve In mathematics, the doubling-oriented Doche–Icart–Kohel curve is a form in which an elliptic curve can be written. It is a special case of Weierstrass form and it is also important in elliptic-curve cryptography because the doubling speeds up considerably .It has been introduced by Christophe... |
7 | 17 | 12 | 6 | |
| Jacobi intersection projective Jacobian curve In mathematics, the Jacobi curve is a representantion of an elliptic curve different than the usual one . Sometimes it is used in cryptography instead of the Weierstrass form because it can provide a defence against simple and differential power analysis style attacks; it is possible, indeed, to... |
7 | 14 | 12 | 6 | 14 |
| Jacobi intersection extended | 7 | 12 | 11 | 7 | 16 |
| Twisted Edwards projective | 7 | 11 | 10 | 6 | |
| Twisted Edwards Inverted | 7 | 10 | 9 | 6 | |
| Twisted Edwards Extended | 8 | 9 | 8 | 7 | |
| Edwards projective | 7 | 11 | 9 | 6 | 13 |
| Jacobi quartic doubling-oriented XXYZZ | 7 | 11 | 9 | 6 | 14 |
| Jacobi quartic XXYZZ | 7 | 11 | 9 | 6 | 14 |
| Jacobi quartic XXYZZR | 7 | 10 | 9 | 7 | 15 |
| Edwards curve inverted | 7 | 10 | 9 | 6 | |
| Montgomery curve | 4 | 3 |


