
Tangent developable
Encyclopedia

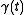 is a ruled surface
is a ruled surfaceRuled surface
In geometry, a surface S is ruled if through every point of S there is a straight line that lies on S. The most familiar examples are the plane and the curved surface of a cylinder or cone...
of the form
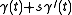 . Intuitively it is the union of the tangent lines to the space curve.
. Intuitively it is the union of the tangent lines to the space curve.A result of Euler states that most developable surface
Developable surface
In mathematics, a developable surface is a surface with zero Gaussian curvature. That is, it is a "surface" that can be flattened onto a plane without distortion . Conversely, it is a surface which can be made by transforming a plane...
s can be obtained as a tangent developable. The exceptions are generalised cones and cylinders and the plane.

