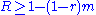
Tanner graph
Encyclopedia
A Tanner graph is a bipartite graph
used to state constraints or equations which specify error correcting codes. In coding theory
, Tanner graphs are used to construct longer codes from smaller ones. Both encoders and decoders employ these graphs extensively.
for product codes.
Tanner discussed lower bounds on the codes obtained from these graphs irrespective of the specific characteristics of the codes which were being used to construct larger codes.
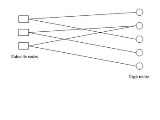
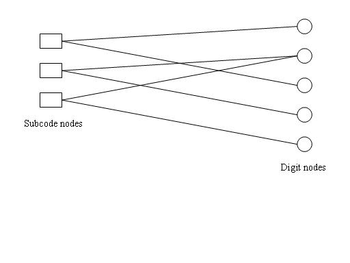Tanner graphs are partitioned
into subcode nodes and digit nodes. For linear block codes, the subcode nodes denote rows of the parity-check matrix
H. The digit nodes represent the columns of the matrix H. An edge connects a subcode node to a digit node if a nonzero entry exists in the intersection of the corresponding row and column.
Let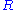
be the rate of the resulting linear code, let the degree of the digit nodes be 
and the degree of the subcode nodes be 
. If each subcode node is associated with a linear code (n,k) with rate r = k/n, then the rate of the code is bounded by
algorithm for Tanner graphs is extremely efficient in practice, although it is not
guaranteed to converge except for cycle-free graphs, which are known not to admit asymptotically
good codes.
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
used to state constraints or equations which specify error correcting codes. In coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, Tanner graphs are used to construct longer codes from smaller ones. Both encoders and decoders employ these graphs extensively.
Origins
Tanner graphs were proposed by Michael Tanner as a means to create larger error correcting codes from smaller ones using recursive techniques. He generalized the techniques of EliasPeter Elias
Peter Elias was a pioneer in the field of information theory. Born in New Brunswick, New Jersey, he was a member of the Massachusetts Institute of Technology faculty from 1953 to 1991....
for product codes.
Tanner discussed lower bounds on the codes obtained from these graphs irrespective of the specific characteristics of the codes which were being used to construct larger codes.
Tanner graphs for Linear block codes
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
into subcode nodes and digit nodes. For linear block codes, the subcode nodes denote rows of the parity-check matrix
Parity-check matrix
In coding theory, a parity-check matrix of a linear block code Cis a generator matrix of the dual code. As such, a codeword c is in C if and only if the matrix-vector product Hc=0....
H. The digit nodes represent the columns of the matrix H. An edge connects a subcode node to a digit node if a nonzero entry exists in the intersection of the corresponding row and column.
Bounds proved by Tanner
Tanner proved the following boundsLet
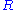be the rate of the resulting linear code, let the degree of the digit nodes be and the degree of the subcode nodes be . If each subcode node is associated with a linear code (n,k) with rate r = k/n, then the rate of the code is bounded by
Computational complexity of Tanner graph based methods
The advantage of these recursive techniques is that they are computationally tractable. The codingalgorithm for Tanner graphs is extremely efficient in practice, although it is not
guaranteed to converge except for cycle-free graphs, which are known not to admit asymptotically
good codes.