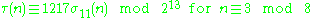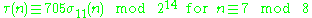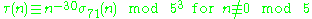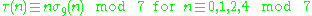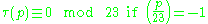Tau-function
Encyclopedia
The Ramanujan tau function, studied by , is the function  defined by the following identity:
defined by the following identity:
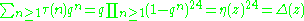 ,
,
where with
with 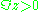 and
and  is the Dedekind eta function
is the Dedekind eta function
and the function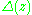 is a holomorphic
is a holomorphic
cusp form
of weight 12 and level 1, known as the discriminant modular form.
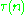 :
:
The first two properties were proved by and the third one, called the Ramanujan conjecture, was proved by Deligne in 1974 as a consequence of his proof of the Weil conjectures
.
Here are some:
For p ≠ 23 prime, we have
Suppose that f is a weight k integer newform and the Fourier coefficients a(n) are integers. Consider the problem: If f does not have complex multplication, prove that almost allprimes p have the property that a(p)≠0 mod p. Indeed, most primes should have this property, and hence they are called ordinary. Despite the big advances by Deligne and Serre on Galois representations, which determine a(n) mod p for n coprime to p, we do not have any clue as to how to compute a(p) mod p.The only theorem in this regard is Elkies' famous result for modular elliptic curves, which indeed guarantees that there are infinitely many primes p for which a(p)=0, which in turn is obviously 0 mod p. We do not know any examples of non-CM f with weight >2 for which a(p)≠0 mod p for infinitely many primes p (although it should be true for almost all p). We also do not know any examples where a(p)=0 mod p for infinitely many p. Some people had begun to doubt whether a(p)=0 mod p indeed for infinitely many p. As evidence, many provided Ramanujan's tau(p) (case of weight 12). The largest known p for which tau(p)=0 mod p is p=7758337633. The only solutions to the equation 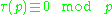 are p = 2, 3, 5, 7, 2411, and 7758337633 up to
are p = 2, 3, 5, 7, 2411, and 7758337633 up to 
Lehmer (1947) conjectured that τ(n)≠0 for all n, an assertion sometimes known as Lehmer's conjecture. Lehmer verified the conjecture for n<214928639999 (Apostol 1997, p. 22). The following table summarizes progress on finding successively larger values of n for which this condition holds.
 defined by the following identity:
defined by the following identity: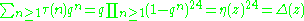 ,
,where
 with
with 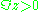 and
and  is the Dedekind eta function
is the Dedekind eta functionDedekind eta function
The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
and the function
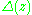 is a holomorphic
is a holomorphicHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
cusp form
Cusp form
In number theory, a branch of mathematics, a cusp form is a particular kind of modular form, distinguished in the case of modular forms for the modular group by the vanishing in the Fourier series expansion \Sigma a_n q^n...
of weight 12 and level 1, known as the discriminant modular form.
Values
The first few values of the tau function are given in the following table :  |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
1 | −24 | 252 | −1472 | 4830 | −6048 | −16744 | 84480 | −113643 | −115920 | 534612 | −370944 | −577738 | 401856 | 1217160 | 987136 |
Ramanujan's conjectures
observed, but could not prove, the following three properties of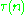 :
:-
 if
if  (meaning that
(meaning that 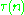 is a multiplicative functionMultiplicative functionIn number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
is a multiplicative functionMultiplicative functionIn number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
) -
 for p prime and r>0.
for p prime and r>0. -
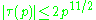 for all primesPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
for all primesPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p.
The first two properties were proved by and the third one, called the Ramanujan conjecture, was proved by Deligne in 1974 as a consequence of his proof of the Weil conjectures
Weil conjectures
In mathematics, the Weil conjectures were some highly-influential proposals by on the generating functions derived from counting the number of points on algebraic varieties over finite fields....
.
Congruences for the tau function
For k ∈ Z and n ∈ Z>0, define σk(n) as the sum of the k-th powers of the divisors of n. The tau functions satisfies several congruence relations; many of them can be expressed in terms of σk(n).Here are some:
For p ≠ 23 prime, we have
Conjectures on tau(n)
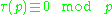 are p = 2, 3, 5, 7, 2411, and 7758337633 up to
are p = 2, 3, 5, 7, 2411, and 7758337633 up to 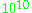
| n | reference |
|---|---|
| 3316799 | Lehmer (1947) |
| 214928639999 | Lehmer (1949) |
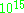 |
Serre (1973, p. 98), Serre (1985) |
| 1213229187071998 | Jennings (1993) |
| 22689242781695999 | Jordan and Kelly (1999) |
| 22798241520242687999 | Bosman (2007) |