Taut submanifold
Encyclopedia
In mathematics
, a (compact) taut submanifold N of a space form
M is a compact
submanifold
with the property that every distance function
for
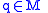
which is a Morse function, is perfect.
If N is not compact, one needs to consider the restriction of the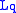
to any of their sublevel sets.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a (compact) taut submanifold N of a space form
Space form
In mathematics, a space form is a complete Riemannian manifold M of constant sectional curvature K. The three obvious examples are Euclidean n-space, the n-dimensional sphere, and hyperbolic space, although a space form need not be simply connected.-Reduction to generalized crystallography:It is a...
M is a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
with the property that every distance function
for
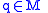
which is a Morse function, is perfect.
If N is not compact, one needs to consider the restriction of the
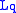to any of their sublevel sets.