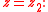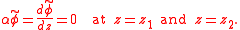Taylor–Goldstein equation
Encyclopedia
The Taylor–Goldstein equation is an ordinary differential equation
used in the fields of geophysical fluid dynamics
, and more generally in fluid dynamics
, in presence of quasi-2D flows. It describes the dynamics
of the Kelvin–Helmholtz instability, subject to buoyancy
forces (e.g. gravity), for stably-stratified fluids in the dissipation-less limit
. Or, more generally, the dynamics of internal waves in the presence of a (continuous) density stratification
and shear flow
. The Taylor–Goldstein equation equation is derived from the 2D Euler equations, using the Boussinesq approximation.
The equation is named after G.I. Taylor
and S. Goldstein
, who derived the equation independently from each other in 1931. The third independent derivation, also in 1931, was made by B. Haurwitz.
The equation is derived by solving a linear
ized version of the Navier–Stokes equation, in presence of gravity
and a mean density gradient (with gradient-length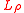 
), for the perturbation velocity field
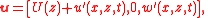
where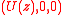
is the unperturbed or basic flow. The perturbation velocity has the wave
-like solution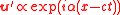
(real part understood). Using this knowledge, and the streamfunction representation
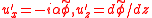for the flow, the following dimensional form of the Taylor–Goldstein equation is obtained:
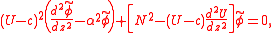
where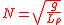
denotes the Brunt–Väisälä frequency. The eigenvalue parameter of the problem is 
. If the imaginary part of the wave speed
is positive, then the flow is unstable, and the small perturbation introduced to the system is amplified in time.
Note that a purely-imaginary
Brunt–Väisälä frequency
results in a flow which is always unstable. This instability is known as the Rayleigh–Taylor instability.
boundary conditions at the channel top and bottom
and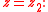 
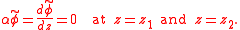
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
used in the fields of geophysical fluid dynamics
Geophysical fluid dynamics
Geophysical fluid dynamics is the study of naturally occurring, large-scale flows on Earth and other planets. It is applied to the motion of fluids in the ocean and outer core, and to gases in the atmosphere of Earth and other planets...
, and more generally in fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, in presence of quasi-2D flows. It describes the dynamics
Dynamics (mechanics)
In the field of physics, the study of the causes of motion and changes in motion is dynamics. In other words the study of forces and why objects are in motion. Dynamics includes the study of the effect of torques on motion...
of the Kelvin–Helmholtz instability, subject to buoyancy
Buoyancy
In physics, buoyancy is a force exerted by a fluid that opposes an object's weight. In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus a column of fluid, or an object submerged in the fluid, experiences greater pressure at the bottom of the...
forces (e.g. gravity), for stably-stratified fluids in the dissipation-less limit
Inviscid flow
In fluid dynamics there are problems that are easily solved by using the simplifying assumption of an ideal fluid that has no viscosity. The flow of a fluid that is assumed to have no viscosity is called inviscid flow....
. Or, more generally, the dynamics of internal waves in the presence of a (continuous) density stratification
Stratification (water)
Water stratification occurs when water masses with different properties - salinity , oxygenation , density , temperature - form layers that act as barriers to water mixing...
and shear flow
Shear flow
The term shear flow is used in solid mechanics as well as in fluid dynamics. Loosely speaking, shear flow is defined as:* the gradient of a shear stress force through the body ;...
. The Taylor–Goldstein equation equation is derived from the 2D Euler equations, using the Boussinesq approximation.
The equation is named after G.I. Taylor
Geoffrey Ingram Taylor
Sir Geoffrey Ingram Taylor OM was a British physicist, mathematician and expert on fluid dynamics and wave theory. His biographer and one-time student, George Batchelor, described him as "one of the most notable scientists of this century".-Biography:Taylor was born in St. John's Wood, London...
and S. Goldstein
Sydney Goldstein
Sydney Goldstein FRS was a British mathematician noted for his contribution to fluid dynamics. He is described as:...
, who derived the equation independently from each other in 1931. The third independent derivation, also in 1931, was made by B. Haurwitz.
Formulation
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
ized version of the Navier–Stokes equation, in presence of gravity
and a mean density gradient (with gradient-length 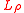), for the perturbation velocity field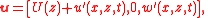where
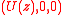is the unperturbed or basic flow. The perturbation velocity has the waveWave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
-like solution
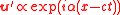(real part understood). Using this knowledge, and the streamfunction representation 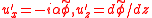for the flow, the following dimensional form of the Taylor–Goldstein equation is obtained: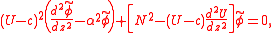where
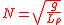denotes the Brunt–Väisälä frequency. The eigenvalue parameter of the problem is . If the imaginary part of the wave speedPhase velocity
The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the speed at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity...
is positive, then the flow is unstable, and the small perturbation introduced to the system is amplified in time.Note that a purely-imaginary
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
Brunt–Väisälä frequency
results in a flow which is always unstable. This instability is known as the Rayleigh–Taylor instability.No-slip boundary conditions
The relevant boundary conditions are, in case of the no-slipNo-slip condition
In fluid dynamics, the no-slip condition for viscous fluids states that at a solid boundary, the fluid will have zero velocity relative to the boundary.The fluid velocity at all fluid–solid boundaries is equal to that of the solid boundary...
boundary conditions at the channel top and bottom
and