TetraVex is a puzzle computer game, available for Windows

Microsoft Windows

Microsoft Windows is a series of operating systems produced by Microsoft.Microsoft introduced an operating environment named Windows on November 20, 1985 as an add-on to MS-DOS in response to the growing interest in graphical user interfaces . Microsoft Windows came to dominate the world's personal...

 and Linux

Linux

Linux is a Unix-like computer operating system assembled under the model of free and open source software development and distribution. The defining component of any Linux system is the Linux kernel, an operating system kernel first released October 5, 1991 by Linus Torvalds...

 systems.

Gameplay

TetraVex is an edge-matching puzzle

Edge-matching puzzle

An edge-matching puzzle is a type of tiling puzzle involving tiling an area with polygons whose edges are distinguished with colours or patterns, in such a way that the edges of adjacent tiles match....

. The player is presented with a grid (by default, 3x3) and nine square tiles, each with a number on each edge. The objective of the game is to place the tiles in the grid in the proper position as fast as possible. Two tiles can only be placed next to each other if the numbers on adjacent faces match.

Availability

TetraVex was originally available for Windows in Windows Entertainment Pack 3. It was later re-released as part of the Best of Windows Entertainment Pack

Best of Windows Entertainment Pack

The Best of Windows Entertainment Pack was a collection of thirteen 16-bit simple games sold separately from Windows. It was published in the Microsoft Home series of software. They were selected as the best games from the previously released Microsoft Entertainment Pack series...

. It is also available as an open source game on the GNOME

GNOME

GNOME is a desktop environment and graphical user interface that runs on top of a computer operating system. It is composed entirely of free and open source software...

 desktop.

Origins

The original version of TetraVex (for the Windows Entertainment Pack 3) was written (and named) by Scott Ferguson who was also the Development Lead and an architect of the first version of Visual Basic. TetraVex was inspired by "the problem of tiling the plane" as described by Donald Knuth

Donald Knuth

Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...

 on page 382 of Volume 1: Fundamental Algorithms, the first book in his The Art of Computer Programming

The Art of Computer Programming

The Art of Computer Programming is a comprehensive monograph written by Donald Knuth that covers many kinds of programming algorithms and their analysis....

 series.

In the TetraVex version for Windows, the Microsoft Blibbet logo is displayed if the player solves a 6 by 6 puzzle.

The tiles are also known as McMahon Squares, named for Percy McMahon

Percy Alexander MacMahon

Percy Alexander MacMahon was a mathematician, especially noted in connection with the partitions of numbers and enumerative combinatorics.-Early life:...

who explored their possibilities in the 1920s.

Counting the possible number of TetraVex

Since the game is simple in its definition, it is easy to count how many possible TetraVex are for each grid of size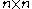 . For instance, if 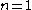, there are 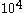possible squares with a number from zero to nine on each edge. Therefore for 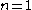there are 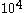possible TetraVex puzzles.

Proposition: There are 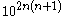possible TetraVex in a grid of size .

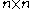Proof sketch: For 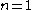this is true. We can proceed with mathematical induction.

Take a grid of 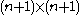. The first rows and the first columns form a grid of 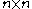and by the hypothesis of induction, there are 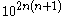possible TetraVex on that subgrid. Now, for each possible TetraVex on the subgrid, we can choose 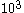squares to be placed in the position 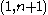of the grid (first row, last column), because only one side is determined. Once this square is chosen, there are 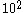squares available to be placed in the position 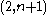, and fixing that square we have 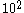possibilities for the square on position 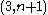. We can go on until the square on position 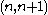is fixed.

The same is true for the last row: there are 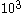possibilities for the square on the first column and last row, and 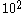for all the other.

This gives us .
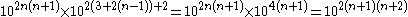Then the proposition is proven by induction.

It is easy to see that if the edges of the squares are allowed to take 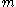possible numbers, then there are 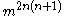possible TetraVex puzzles.