The Sand Reckoner
Encyclopedia
The Sand Reckoner is a work by Archimedes
in which he set out to determine an upper bound for the number of grains of sand that fit into the universe
. In order to do this, he had to estimate the size of the universe according to the then-current model, and invent a way to talk about extremely large numbers. The work, also known in Latin as Archimedis Syracusani Arenarius & Dimensio Circuli, is about 8 pages long in translation, is addressed to the Syracusan king Gelo II
(son of Hiero II
), and is probably the most accessible work of Archimedes
; in some sense, it is the first research-expository paper.
. The number system in use at that time could express numbers up to a myriad
(μυριάς — 10,000), and by utilizing the word "myriad" itself, one can immediately extend this to naming all numbers up to a myriad myriads (108). Archimedes called the numbers up to 108 "first numbers" and called 108 itself the "unit of the second numbers". Multiples of this unit then became the second numbers, up to this unit taken a myriad-myriad times, 108·108=1016. This became the "unit of the third numbers", whose multiples were the third numbers, and so on. Archimedes continued naming numbers in this way up to a myriad-myriad times the unit of the 108-th numbers, i.e.,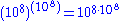
.
After having done this, Archimedes called the numbers he had defined the "numbers of the first period", and called the last one,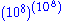
, the "unit of the second period". He then constructed the numbers of the second period by taking multiples of this unit in a way analogous to the way in which the numbers of the first period were constructed. Continuing in this manner, he eventually arrived at the numbers of the myriad-myriadth period. The largest number named by Archimedes was the last number in this period, which is
Another way of describing this number is a one followed by (short scale
) eighty quadrillion
(80·1015) zeroes.
Archimedes' system is reminiscent of a positional numeral system with base 108, which is remarkable because the ancient Greeks used a very simple system for writing numbers
, which employs 27 different letters of the alphabet for the units 1 through 9, the tens 10 through 90 and the hundreds 100 through 900.
Archimedes also discovered and proved the law of exponents
,
, necessary to manipulate powers of 10.
. (This work by Aristarchus has been lost; Archimedes' work is one of the few surviving references to his theory.) The reason for the large size of this model is that the Greeks were unable to observe stellar parallax
with available techniques, which implies that any parallax is extremely subtle and so the stars must be placed at great distances from the Earth (assuming heliocentrism
to be true).
According to Archimedes, Aristarchus did not state how far the stars were from the Earth. Archimedes therefore had to make an assumption; he assumed that the Universe was spherical and that the ratio of the diameter of the Universe to the diameter of the orbit of the Earth around the Sun equalled the ratio of the diameter of the orbit of the Earth around the Sun to the diameter of the Earth. This assumption can also be expressed by saying that the stellar parallax caused by the motion of the Earth around its orbit equals the solar parallax caused by motion around the Earth.
In order to obtain an upper bound, Archimedes used overestimates of his data by assuming:
Archimedes then computed that the diameter of the Universe was no more than 1014 stadia (in modern units, about 2 light years), and that it would require no more than 1063 grains of sand to fill it.
Archimedes made some interesting experiments and computations along the way. One experiment was to estimate the angular size of the Sun, as seen from the Earth. Archimedes' method is especially interesting as it takes into account the finite size of the eye's pupil, and therefore may be the first known example of experimentation in psychophysics
, the branch of psychology
dealing with the mechanics of human perception, whose development is generally attributed to Hermann von Helmholtz
. Another interesting computation accounts for solar parallax and the different distances between the viewer and the Sun, whether viewed from the center of the Earth or from the surface of the Earth at sunrise. This may be the first known computation dealing with solar parallax.
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
in which he set out to determine an upper bound for the number of grains of sand that fit into the universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
. In order to do this, he had to estimate the size of the universe according to the then-current model, and invent a way to talk about extremely large numbers. The work, also known in Latin as Archimedis Syracusani Arenarius & Dimensio Circuli, is about 8 pages long in translation, is addressed to the Syracusan king Gelo II
Gelo, son of Hiero II
Gelo, son of Hiero II was the eldest son of Hiero II, tyrant of Syracuse. After the huge defeat suffered by the Romans at Cannae, Gelo went over to the Carthaginian side and began making friendly overtures to the cities allied to Rome. Not long after these events, in 216 BC Gelo died. Livy suggests...
(son of Hiero II
Hiero II of Syracuse
Hieron II , king of Syracuse from 270 to 215 BC, was the illegitimate son of a Syracusan noble, Hierocles, who claimed descent from Gelon. He was a former general of Pyrrhus of Epirus and an important figure of the First Punic War....
), and is probably the most accessible work of Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
; in some sense, it is the first research-expository paper.
Naming large numbers
First, Archimedes had to invent a system of naming large numbersLarge numbers
This article is about large numbers in the sense of numbers that are significantly larger than those ordinarily used in everyday life, for instance in simple counting or in monetary transactions...
. The number system in use at that time could express numbers up to a myriad
Myriad
Myriad , "numberlesscountless, infinite", is a classical Greek word for the number 10,000. In modern English, the word refers to an unspecified large quantity.-History and usage:...
(μυριάς — 10,000), and by utilizing the word "myriad" itself, one can immediately extend this to naming all numbers up to a myriad myriads (108). Archimedes called the numbers up to 108 "first numbers" and called 108 itself the "unit of the second numbers". Multiples of this unit then became the second numbers, up to this unit taken a myriad-myriad times, 108·108=1016. This became the "unit of the third numbers", whose multiples were the third numbers, and so on. Archimedes continued naming numbers in this way up to a myriad-myriad times the unit of the 108-th numbers, i.e.,
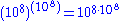.After having done this, Archimedes called the numbers he had defined the "numbers of the first period", and called the last one,
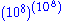, the "unit of the second period". He then constructed the numbers of the second period by taking multiples of this unit in a way analogous to the way in which the numbers of the first period were constructed. Continuing in this manner, he eventually arrived at the numbers of the myriad-myriadth period. The largest number named by Archimedes was the last number in this period, which is
Another way of describing this number is a one followed by (short scale
Long and short scales
The long and short scales are two of several different large-number naming systems used throughout the world for integer powers of ten. Many countries, including most in continental Europe, use the long scale whereas most English-speaking countries use the short scale...
) eighty quadrillion
Quadrillion
Quadrillion may mean either of the two numbers :* 1,000,000,000,000,000 – for all short scale countries; increasingly common meaning in English language usage* 1,000,000,000,000,000,000,000,000 – for all...
(80·1015) zeroes.
Archimedes' system is reminiscent of a positional numeral system with base 108, which is remarkable because the ancient Greeks used a very simple system for writing numbers
Greek numerals
Greek numerals are a system of representing numbers using letters of the Greek alphabet. They are also known by the names Ionian numerals, Milesian numerals , Alexandrian numerals, or alphabetic numerals...
, which employs 27 different letters of the alphabet for the units 1 through 9, the tens 10 through 90 and the hundreds 100 through 900.
Archimedes also discovered and proved the law of exponents
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
,
, necessary to manipulate powers of 10.Estimation of the size of the universe
Archimedes then estimated an upper bound for the number of grains of sand required to fill the Universe. To do this, he used the heliocentric model of Aristarchus of SamosAristarchus of Samos
Aristarchus, or more correctly Aristarchos , was a Greek astronomer and mathematician, born on the island of Samos, in Greece. He presented the first known heliocentric model of the solar system, placing the Sun, not the Earth, at the center of the known universe...
. (This work by Aristarchus has been lost; Archimedes' work is one of the few surviving references to his theory.) The reason for the large size of this model is that the Greeks were unable to observe stellar parallax
Stellar parallax
Stellar parallax is the effect of parallax on distant stars in astronomy. It is parallax on an interstellar scale, and it can be used to determine the distance of Earth to another star directly with accurate astrometry...
with available techniques, which implies that any parallax is extremely subtle and so the stars must be placed at great distances from the Earth (assuming heliocentrism
Heliocentrism
Heliocentrism, or heliocentricism, is the astronomical model in which the Earth and planets revolve around a stationary Sun at the center of the universe. The word comes from the Greek . Historically, heliocentrism was opposed to geocentrism, which placed the Earth at the center...
to be true).
According to Archimedes, Aristarchus did not state how far the stars were from the Earth. Archimedes therefore had to make an assumption; he assumed that the Universe was spherical and that the ratio of the diameter of the Universe to the diameter of the orbit of the Earth around the Sun equalled the ratio of the diameter of the orbit of the Earth around the Sun to the diameter of the Earth. This assumption can also be expressed by saying that the stellar parallax caused by the motion of the Earth around its orbit equals the solar parallax caused by motion around the Earth.
In order to obtain an upper bound, Archimedes used overestimates of his data by assuming:
- that the perimeter of the Earth was no bigger than 300 myriad stadia (~5·105 km).
- that the Moon was no larger than the Earth, and that the Sun was no more than thirty times larger than the Moon.
- that the angular diameter of the Sun, as seen from the Earth, was greater than 1/200th of a right angle.
Archimedes then computed that the diameter of the Universe was no more than 1014 stadia (in modern units, about 2 light years), and that it would require no more than 1063 grains of sand to fill it.
Archimedes made some interesting experiments and computations along the way. One experiment was to estimate the angular size of the Sun, as seen from the Earth. Archimedes' method is especially interesting as it takes into account the finite size of the eye's pupil, and therefore may be the first known example of experimentation in psychophysics
Psychophysics
Psychophysics quantitatively investigates the relationship between physical stimuli and the sensations and perceptions they effect. Psychophysics has been described as "the scientific study of the relation between stimulus and sensation" or, more completely, as "the analysis of perceptual...
, the branch of psychology
Psychology
Psychology is the study of the mind and behavior. Its immediate goal is to understand individuals and groups by both establishing general principles and researching specific cases. For many, the ultimate goal of psychology is to benefit society...
dealing with the mechanics of human perception, whose development is generally attributed to Hermann von Helmholtz
Hermann von Helmholtz
Hermann Ludwig Ferdinand von Helmholtz was a German physician and physicist who made significant contributions to several widely varied areas of modern science...
. Another interesting computation accounts for solar parallax and the different distances between the viewer and the Sun, whether viewed from the center of the Earth or from the surface of the Earth at sunrise. This may be the first known computation dealing with solar parallax.