Thermal capillary wave
Encyclopedia
Thermal motion is able to produce capillary waves at the molecular scale. At this scale,
gravity and hydrodynamics can be neglected, and only the surface tension
contribution is
relevant.
Capillary wave theory (CWT) is a classic account of how thermal fluctuations
distort an interface.
It starts from some intrinsic surface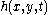
that is distorted. Its energy will be
proportional to its area:
where the first equality is the area in this (the Monge
) representation, and the second
applies for small values of the derivatives (surfaces not too rough). The constant of proportionality,
, is the surface tension
.
By performing a Fourier analysis treatment, normal modes are easily found. Each contributes an energy proportional to the square of its amplitude; therefore, according to classical statistical mechanics, equipartition holds, and the mean energy of each mode will be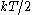
. Surprisingly, this result leads to a divergent surface (the width of the interface is bound to diverge with its area). This divergence is nevertheless very mild: even for displacements on the order of meters the deviation of the surface is comparable to the size of the molecules. Moreover, the introduction of an external field removes the divergence: the action of gravity is sufficient to keep the width fluctuation on the order of one molecular diameter for areas larger than about 1 mm2 (Ref. 2). .
gravity and hydrodynamics can be neglected, and only the surface tension
Surface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
contribution is
relevant.
Capillary wave theory (CWT) is a classic account of how thermal fluctuations
Thermal fluctuations
In statistical mechanics, thermal fluctuations are random deviations of a system from its equilibrium. All thermal fluctuations become larger and more frequent as the temperature increases, and likewise they disappear altogether as temperature approaches absolute zero.Thermal fluctuations are a...
distort an interface.
It starts from some intrinsic surface
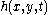that is distorted. Its energy will beproportional to its area:
where the first equality is the area in this (the Monge
Gaspard Monge
Gaspard Monge, Comte de Péluse was a French mathematician, revolutionary, and was inventor of descriptive geometry. During the French Revolution, he was involved in the complete reorganization of the educational system, founding the École Polytechnique...
) representation, and the second
applies for small values of the derivatives (surfaces not too rough). The constant of proportionality,
, is the surface tensionSurface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
.
By performing a Fourier analysis treatment, normal modes are easily found. Each contributes an energy proportional to the square of its amplitude; therefore, according to classical statistical mechanics, equipartition holds, and the mean energy of each mode will be
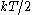. Surprisingly, this result leads to a divergent surface (the width of the interface is bound to diverge with its area). This divergence is nevertheless very mild: even for displacements on the order of meters the deviation of the surface is comparable to the size of the molecules. Moreover, the introduction of an external field removes the divergence: the action of gravity is sufficient to keep the width fluctuation on the order of one molecular diameter for areas larger than about 1 mm2 (Ref. 2). .