Theta representation
Encyclopedia
In mathematics
, the theta representation is a particular representation of the Heisenberg group of quantum mechanics
. It gains its name from the fact that the Jacobi theta function is invariant under the action of a discrete subgroup of the Heisenberg group. The representation was popularized by David Mumford
.
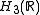over the field of the real numbers. In this representation, the group elements act on a particular Hilbert space
. The construction below proceeds first by defining operators that correspond to the Heisenberg group generators. Next, the Hilbert space on which these act is defined, followed by a demonstration of the isomorphism
to the usual representations.
, let a and b be real number
s, and let
be fixed, but arbitrary complex number in the upper half-plane; that is, so that the imaginary part of 
is positive. Define the operators Sa and Tb such that they act on holomorphic functions as
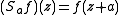
and
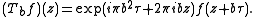
It can be seen that each operator generates a one-parameter subgroup:
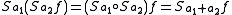
and
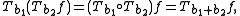
However, S and T do not commute:
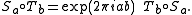
Thus we see that S and T together with a unitary
phase form a nilpotent
Lie group
, the (continuous real) Heisenberg group, parametrizable as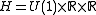
where U(1) is the unitary group
. A general group element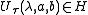
then acts on a holomorphic function f(z) as
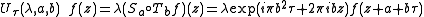
where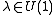
. U(1) = Z(H) is the center of H, the commutator subgroup
[H, H]. The parameter
on 
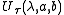serves only to remind that every different value of 
gives rise to a different representation of the action of the group.
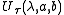is unitary and irreducible on a certain Hilbert space of functions. For a fixed value of τ, define a norm on entire function
s of the complex plane
as
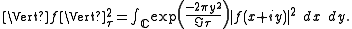
Here,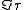
is the imaginary part of 
and the domain of integration is the entire complex plane. Let 
be the set of entire functions f with finite norm. The subscript 
is used only to indicate that the space depends on the choice of parameter 
. This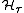 
forms a Hilbert space
. The action of
given above is unitary on 
, that is,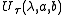 
preserves the norm on this space. Finally, the action of 
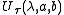on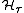 
is irreducible.
and L2(R)
are isomorphic as H-modules
. Let
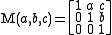
stand for a general group element of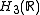
. In the canonical Weyl representation, for every real number h, there is a representation 
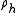acting on L2(R) as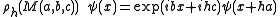
for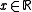
and 
.
Here, h is Planck's constant. Each such representation is unitarily inequivalent. The corresponding theta representation is:
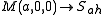
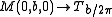
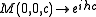
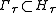as
The Jacobi theta function is defined as
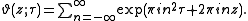
It is an entire function
of z that is invariant
under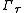
. This follows from the properties of the theta function:
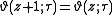
and
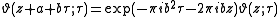
when a and b are integers. It can be shown that the Jacobi theta is the unique such function.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the theta representation is a particular representation of the Heisenberg group of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. It gains its name from the fact that the Jacobi theta function is invariant under the action of a discrete subgroup of the Heisenberg group. The representation was popularized by David Mumford
David Mumford
David Bryant Mumford is an American mathematician known for distinguished work in algebraic geometry, and then for research into vision and pattern theory. He won the Fields Medal and was a MacArthur Fellow. In 2010 he was awarded the National Medal of Science...
.
Construction
The theta representation is a representation of the continuous Heisenberg group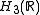 over the field of the real numbers. In this representation, the group elements act on a particular Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. The construction below proceeds first by defining operators that correspond to the Heisenberg group generators. Next, the Hilbert space on which these act is defined, followed by a demonstration of the isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to the usual representations.
Group generators
Let f(z) be a holomorphic functionHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
, let a and b be real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, and let
be fixed, but arbitrary complex number in the upper half-plane; that is, so that the imaginary part of is positive. Define the operators Sa and Tb such that they act on holomorphic functions as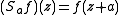and
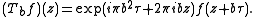
It can be seen that each operator generates a one-parameter subgroup:
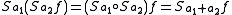
and
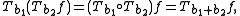
However, S and T do not commute:
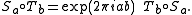
Thus we see that S and T together with a unitary
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
phase form a nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, the (continuous real) Heisenberg group, parametrizable as
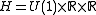where U(1) is the unitary groupUnitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
. A general group element
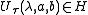then acts on a holomorphic function f(z) as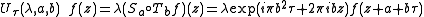where
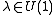. U(1) = Z(H) is the center of H, the commutator subgroupCommutator subgroup
In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
[H, H]. The parameter
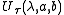on serves only to remind that every different value of gives rise to a different representation of the action of the group.Hilbert space
The action of the group elements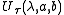 is unitary and irreducible on a certain Hilbert space of functions. For a fixed value of τ, define a norm on entire functionEntire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
s of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
as
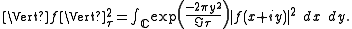
Here,
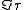is the imaginary part of and the domain of integration is the entire complex plane. Let be the set of entire functions f with finite norm. The subscript is used only to indicate that the space depends on the choice of parameter . This 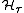forms a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. The action of
given above is unitary on , that is, 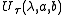preserves the norm on this space. Finally, the action of 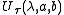on 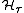is irreducible.Isomorphism
The above theta representation of the Heisenberg group is isomorphic to the canonical Weyl representation of the Heisenberg group. In particular, this implies that and L2(R)Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
are isomorphic as H-modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
. Let
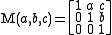
stand for a general group element of
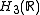. In the canonical Weyl representation, for every real number h, there is a representation 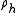acting on L2(R) as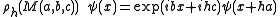for
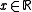and .Here, h is Planck's constant. Each such representation is unitarily inequivalent. The corresponding theta representation is:
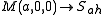
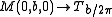
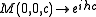
Discrete subgroup
Define the subgroup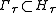 asThe Jacobi theta function is defined as
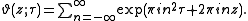
It is an entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
of z that is invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
under
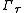. This follows from the properties of the theta function: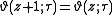and
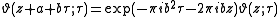
when a and b are integers. It can be shown that the Jacobi theta is the unique such function.