
Time-dependent density functional theory
Encyclopedia
Time-dependent density functional theory (TDDFT) is a quantum mechanical theory used in physics and chemistry to investigate the properties and dynamics
of many-body systems in the presence of time-dependent potentials, such as electric or magnetic fields. The effect of such fields on molecules and solids can be studied with TDDFT to extract features like excitation energies, frequency-dependent response properties, and photoabsorption spectra.
TDDFT is an extension of density functional theory
(DFT), and the conceptual and computational foundations are analogous – to show that the (time-dependent) wave function is equivalent to the (time-dependent) electronic density
, and then to derive the effective potential of a fictitious non-interacting system which returns the same density as any given interacting system. The issue of constructing such a system is more complex for TDDFT, most notably because the time-dependent effective potential at any given instant depends on value of the density at all previous times. Consequently the development of time-dependent approximations for the implementation of TDDFT is behind that of DFT, with applications routinely ignoring this memory requirement.
Given the RG theorem, the next step in developing a computationally useful method is to determine the fictitious non-interacting system which has the same density as the physical (interacting) system of interest. As in DFT, this is called the (time-dependent) Kohn-Sham system. This system is formally found as the stationary point
of an action
functional defined in the Keldysh formalism
.
The most popular application of TDDFT is in the calculation of the energies of excited states of isolated systems and, less commonly, solids. Such calculations are based on the fact that the linear response function – that is, how the electron density changes when the external potential changes – has poles at the exact excitation energies of a system. Such calculations require, in addition to the exchange-correlation potential, the exchange-correlation kernel – the functional derivative
of the exchange-correlation potential with respect to the density.
for which the Hamiltonian
takes the form
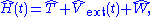
where T is the kinetic energy operator, W the electron-electron interaction, and Vext(t) the external potential which along with the number of electrons defines the system. Nominally, the external potential contains the electrons' interaction with the nuclei of the system. For non-trivial time-dependence, an additional explicitly time-dependent potential is present which can arise, for example, from a time-dependent electric or magnetic field. The many-body wavefunction evolves according to the time-dependent Schrödinger equation under a single initial condition,
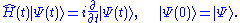
Employing the Schrödinger equation as its starting point, the Runge-Gross theorem shows that at any time, the density uniquely determines the external potential. This is done in two steps:
of single-particle orbitals
, each of which are determined by a single partial differential equation
in three variable – and that the kinetic energy of a non-interacting system can be expressed exactly in terms of those orbitals. The problem is thus to determine a potential, denoted as vs(r,t) or vKS(r,t), that determines a non-interacting Hamiltonian, Hs,
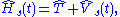
which in turn determines a determinantal wave function
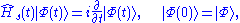
which is constructed in terms of a set of N orbitals which obey the equation,
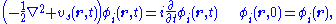
and generate a time-dependent density

such that ρs is equal to the density of the interacting system at all times:
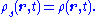
If the potential vs(r,t) can be determined, or at the least well-approximated, then the original Schrödinger equation, a single partial differential equation in 3N variables, has been replaced by N differential equations in 3 dimensions, each differing only in the initial condition.
The problem of determining approximations to the Kohn-Sham potential is challenging. Analogously to DFT, the time-dependent KS potential is decomposed to extract the external potential of the system and the time-dependent Coulomb interaction, vJ. The remaining component is the exchange-correlation potential:

In their seminal paper, Runge and Gross approached the definition of the KS potential through an action-based argument starting from the Dirac action
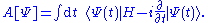
Treated as a functional of the wave function, A[Ψ], variations of the wave function yield the many-body Schrödinger equation as the stationary point. Given the unique mapping between densities and wave function, Runge and Gross then treated the Dirac action as a density functional,

and derived a formal expression for the exchange-correlation component of the action, which determines the exchange-correlation potential by functional differentiation. Later it was observed that an approach based on the Dirac action yields paradoxical conclusions when considering the causality of the response functions it generates. The density response function, the functional derivative of the density with respect to the external potential, should be causal: a change in the potential at a given time can not effect the density at earlier times. The response functions from the Dirac action however are symmetric in time so lack the required causal structure. An approach which does not suffer from this issue was later introduced with through an action based on the Keldysh formalism
of complex-time path integration.
sense that it does not completely destroy the ground-state structure of the system. In this case
one can analyze the linear response of the system. This is a great advantage as, to first order,
the variation of the system will depend only on the ground-state wave-function so that we can
simply use all the properties of DFT.
Consider a small time-dependent external perturbation .
.
This gives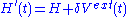
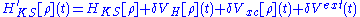
and looking at the linear response of the density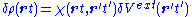
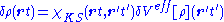
where
Here and in the following it is assumed that primed variables are integrated.
Within the linear-response domain, the variation of the Hartree (H) and the
exchange-correlation (xc) potential to linear order may be expanded with respect to the density variation
and
Finally, inserting this relation in the response equation for the KS system and comparing
the resultant equation with the response equation for the physical system yields the Dyson
equation of TDDFT: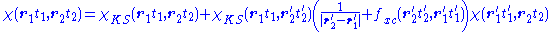
From this last equation it is possible to derive the excitation energies of the system, as these are simply the poles of the response function.
Other linear-response approaches include the Casida formalism (an expansion in electron-hole pairs) and the Sternheimer equation (density-functional perturbation theory).
Molecular dynamics
Molecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
of many-body systems in the presence of time-dependent potentials, such as electric or magnetic fields. The effect of such fields on molecules and solids can be studied with TDDFT to extract features like excitation energies, frequency-dependent response properties, and photoabsorption spectra.
TDDFT is an extension of density functional theory
Density functional theory
Density functional theory is a quantum mechanical modelling method used in physics and chemistry to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. With this theory, the properties of a many-electron system can be determined by...
(DFT), and the conceptual and computational foundations are analogous – to show that the (time-dependent) wave function is equivalent to the (time-dependent) electronic density
Electronic density
In quantum mechanics, and in particular quantum chemistry, the electronic density is a measure of the probability of an electron occupying an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial variables and is typically denoted as either...
, and then to derive the effective potential of a fictitious non-interacting system which returns the same density as any given interacting system. The issue of constructing such a system is more complex for TDDFT, most notably because the time-dependent effective potential at any given instant depends on value of the density at all previous times. Consequently the development of time-dependent approximations for the implementation of TDDFT is behind that of DFT, with applications routinely ignoring this memory requirement.
Overview
The formal foundation of TDDFT is the Runge-Gross (RG) theorem (1984) – the time-dependent analogue of the Hohenberg-Kohn (HK) theorem (1964). The RG theorem shows that, for a given initial wavefunction, there is a unique mapping between the time-dependent external potential of a system and its time-dependent density. This implies that the many-body wavefunction, depending upon 3N variables, is equivalent to the density, which depends upon only 3, and that all properties of a system can thus be determined from knowledge of the density alone. Unlike in DFT, there is no general minimization principle in time-dependent quantum mechanics. Consequently the proof of the RG theorem is more involved than the HK theorem.Given the RG theorem, the next step in developing a computationally useful method is to determine the fictitious non-interacting system which has the same density as the physical (interacting) system of interest. As in DFT, this is called the (time-dependent) Kohn-Sham system. This system is formally found as the stationary point
Stationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
of an action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
functional defined in the Keldysh formalism
Keldysh formalism
In condensed matter physics, the Keldysh formalism is a general framework for describing the quantum mechanical evolution of a system in a non-equilibrium state, e.g. in the presence of time varying fields . The main mathematical object in the Keldysh formalism is the non-equilibrium Green's...
.
The most popular application of TDDFT is in the calculation of the energies of excited states of isolated systems and, less commonly, solids. Such calculations are based on the fact that the linear response function – that is, how the electron density changes when the external potential changes – has poles at the exact excitation energies of a system. Such calculations require, in addition to the exchange-correlation potential, the exchange-correlation kernel – the functional derivative
Functional derivative
In mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
of the exchange-correlation potential with respect to the density.
Runge-Gross theorem
The approach of Runge and Gross considers a single-component system in the presence of a time-dependent scalar fieldScalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
for which the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
takes the form
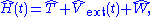
where T is the kinetic energy operator, W the electron-electron interaction, and Vext(t) the external potential which along with the number of electrons defines the system. Nominally, the external potential contains the electrons' interaction with the nuclei of the system. For non-trivial time-dependence, an additional explicitly time-dependent potential is present which can arise, for example, from a time-dependent electric or magnetic field. The many-body wavefunction evolves according to the time-dependent Schrödinger equation under a single initial condition,
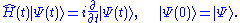
Employing the Schrödinger equation as its starting point, the Runge-Gross theorem shows that at any time, the density uniquely determines the external potential. This is done in two steps:
- Assuming that the external potential can be expanded in a Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
about a given time, it is shown that two external potentials differing by more than an additive constant generate different current densitiesCurrent densityCurrent density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
. - Employing the continuity equationContinuity equationA continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
, it is then shown that for finite systems, different current densities correspond to different electron densities.
Time-dependent Kohn-Sham system
For a given interaction potential, the RG theorem shows that the external potential uniquely determines the density. The Kohn-Sham approaches chooses a non-interacting system (that for which the interaction potential is zero) in which to form the density that is equal to the interacting system. The advantage of doing so lies in the ease in which non-interacting systems can be solved – the wave function of a non-interacting system can be represented as a Slater determinantSlater determinant
In quantum mechanics, a Slater determinant is an expression that describes the wavefunction of a multi-fermionic system that satisfies anti-symmetry requirements and consequently the Pauli exclusion principle by changing sign upon exchange of fermions . It is named for its discoverer, John C...
of single-particle orbitals
Molecular orbital
In chemistry, a molecular orbital is a mathematical function describing the wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The term "orbital" was first...
, each of which are determined by a single partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
in three variable – and that the kinetic energy of a non-interacting system can be expressed exactly in terms of those orbitals. The problem is thus to determine a potential, denoted as vs(r,t) or vKS(r,t), that determines a non-interacting Hamiltonian, Hs,
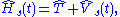
which in turn determines a determinantal wave function
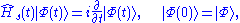
which is constructed in terms of a set of N orbitals which obey the equation,
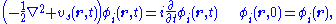
and generate a time-dependent density

such that ρs is equal to the density of the interacting system at all times:
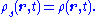
If the potential vs(r,t) can be determined, or at the least well-approximated, then the original Schrödinger equation, a single partial differential equation in 3N variables, has been replaced by N differential equations in 3 dimensions, each differing only in the initial condition.
The problem of determining approximations to the Kohn-Sham potential is challenging. Analogously to DFT, the time-dependent KS potential is decomposed to extract the external potential of the system and the time-dependent Coulomb interaction, vJ. The remaining component is the exchange-correlation potential:

In their seminal paper, Runge and Gross approached the definition of the KS potential through an action-based argument starting from the Dirac action
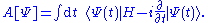
Treated as a functional of the wave function, A[Ψ], variations of the wave function yield the many-body Schrödinger equation as the stationary point. Given the unique mapping between densities and wave function, Runge and Gross then treated the Dirac action as a density functional,

and derived a formal expression for the exchange-correlation component of the action, which determines the exchange-correlation potential by functional differentiation. Later it was observed that an approach based on the Dirac action yields paradoxical conclusions when considering the causality of the response functions it generates. The density response function, the functional derivative of the density with respect to the external potential, should be causal: a change in the potential at a given time can not effect the density at earlier times. The response functions from the Dirac action however are symmetric in time so lack the required causal structure. An approach which does not suffer from this issue was later introduced with through an action based on the Keldysh formalism
Keldysh formalism
In condensed matter physics, the Keldysh formalism is a general framework for describing the quantum mechanical evolution of a system in a non-equilibrium state, e.g. in the presence of time varying fields . The main mathematical object in the Keldysh formalism is the non-equilibrium Green's...
of complex-time path integration.
Linear response TDDFT
Linear-response TDDFT can be used if the external perturbation is small in thesense that it does not completely destroy the ground-state structure of the system. In this case
one can analyze the linear response of the system. This is a great advantage as, to first order,
the variation of the system will depend only on the ground-state wave-function so that we can
simply use all the properties of DFT.
Consider a small time-dependent external perturbation
 .
.This gives
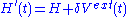
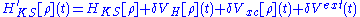
and looking at the linear response of the density
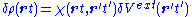
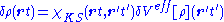
where

Here and in the following it is assumed that primed variables are integrated.
Within the linear-response domain, the variation of the Hartree (H) and the
exchange-correlation (xc) potential to linear order may be expanded with respect to the density variation

and

Finally, inserting this relation in the response equation for the KS system and comparing
the resultant equation with the response equation for the physical system yields the Dyson
equation of TDDFT:
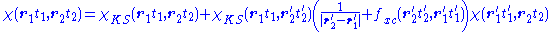
From this last equation it is possible to derive the excitation energies of the system, as these are simply the poles of the response function.
Other linear-response approaches include the Casida formalism (an expansion in electron-hole pairs) and the Sternheimer equation (density-functional perturbation theory).
Key papers
- P. Hohenberg and W. Kohn, Phys. Rev. 136 (1964) B864
- E. Runge and E.K.U. Gross, Phys. Rev. Lett. 52 (1984) 997
Books on TDDFT
- M.A.L. Marques, C.A. Ullrich, F. Nogueira, A. Rubio, K. Burke, and E.K.U. Gross (eds.), Time-Dependent Density Functional Theory (Springer-Verlag, 2006). ISBN 978-3-540-35422-2
TDDFT codes
- Amsterdam Density FunctionalAmsterdam Density FunctionalAmsterdam Density Functional is a program for first-principles electronic structure calculations that makes use of density functional theory . ADF was first developed in the early seventies by the group of E. J. Baerends from the Vrije Universiteit in Amsterdam, and by the group of T. Ziegler...
- CP2KCP2KCP2K is a freely available program, written in Fortran 95, to perform atomistic and molecular simulations of solid state, liquid, molecular and biological systems...
- Dalton (program)
- GAUSSIANGAUSSIANGaussian is a computational chemistry software program initially released in 1970 by John Pople and his research group at Carnegie-Mellon University as Gaussian 70. It has been continuously updated since then...
- NWChemNWChemNWChem is an ab initio computational chemistry software package which also includes quantum chemical and molecular dynamics functionality.It was designed to run on high-performance parallel supercomputers as well as conventional workstation clusters. It aims to be scalable both in its ability to...
- Octopus
- PARSECPARSECPARSEC is a package designed to perform electronic structure calculations of solids and molecules using density functional theory . The acronym stands for Pseudopotential Algorithm for Real-Space Electronic Calculations....
- Q-ChemQ-ChemQ-Chem is an ab initio computational chemistry software program. Q-Chem can perform a number of general quantum chemistry calculations, including Hartree-Fock, density functional theory , coupled cluster , configuration interaction and other advanced electronic structure methods...
- SpartanSpartan (software)SPARTAN is a molecular modeling and computational chemistry application from . It contains code for molecular mechanics, semi-empirical methods, ab initio models, density functional models, post-Hartree-Fock models, and thermochemical recipes including T1....
- TeraChemTeraChemTeraChem is the first computational chemistry software program written completely from scratch to benefit from the new streaming processors such as Graphics Processing Units . The computational algorithms have been completely redesigned to exploit massive parallelism of CUDA-enabled NVIDIA GPUs...
- TURBOMOLETURBOMOLETURBOMOLE is an ab initio computational chemistry program that implements various quantum chemistry algorithms. It is developed at the group of Prof. Reinhart Ahlrichs at the University of Karlsruhe....
- YAMBO codeYAMBO codeYambo is an open source Many-body theory software package for study solids and molecular systems. It calculates the excited state properties of physical systems from first principles Yambo is an open source Many-body theory software package for study solids and molecular systems. It...
- ORCA

