Time-frequency representation
Encyclopedia
A time–frequency representation (TFR) is a view of a signal
(taken to be a function of time) represented over both time and frequency
. Time–frequency analysis means analysis into the time–frequency domain provided by a TFR. This is achieved by using a formulation often called "Time–Frequency Distribution", abbreviated as TFD.
TFRs are often complex-valued fields over time and frequency, where the modulus of the field represents "energy density" (the concentration of the root mean square
over time and frequency) or amplitude, and the argument of the field represents phase.
, as a function
of time, may be considered as a representation with perfect time resolution.
In contrast, the magnitude
of the Fourier transform
(FT) of the signal may be considered as a representation with perfect spectral resolution but with no time information because the magnitude of the FT conveys frequency content but it fails to convey when, in time, different events occur in the signal.
TFRs provide a bridge between these two representations in that they provide some temporal information and some spectral information simultaneously. Thus, TFRs are useful for the representation and analysis of signals containing multiple time-varying frequencies.
TFRs or TFDs (QTFRs or QTFDs) because the representation is quadratic in the signal. This formulation was first described by Eugene Wigner in 1932 in the context of quantum mechanics
and, later, reformulated as a general TFR by Ville in 1948 to form what is now known as the Wigner–Ville distribution, as it was shown in that Wigner's formula needed to use the anaytic signal defined in Ville's paper to be useful as a representation and for a practical analysis. Today, various QTFRs include but not limited to spectrogram
(squared magnitude of short-time Fourier transform
), scaleogram
(squared magnitude of Wavelet transform) and the smoothed pseudo-Wigner distribution. In fact, a whole class of representations using bilinear time–frequency distributions fall in this category.
Although quadratic TFRs offer perfect temporal and spectral resolutions simultaneously, the quadratic nature of the transforms creates cross-terms. The following can be used to estimate which QTFRs contain cross terms.
Given a QTFR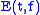
defined on 
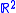, define a constant 
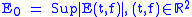and a set 
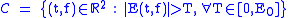. The QTFR, 
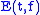is cross-term free if 
is a convex set
.
The windowed Fourier transform (also known as the short-time Fourier transform
) localises the signal by modulating it with a window function, before performing the Fourier transform to obtain the frequency content of the signal in the region of the window.
, expand the signal in terms of wavelet functions which are localised in both time and frequency. Thus the wavelet transform of a signal may be represented in terms of both time and frequency.
The notions of time, frequency, and amplitude used to generate a TFR from a wavelet transform were originally developed intuitively. In 1992, Delprat et al. gave a quantitative derivation of these relationships, based upon a stationary phase approximation.
s are the linear transforms of the time–frequency representation that preserve the symplectic form. These include and generalize the Fourier transform
, fractional Fourier transform
, and others, thus providing a unified view of these transforms in terms of their action on the time–frequency domain.
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
(taken to be a function of time) represented over both time and frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
. Time–frequency analysis means analysis into the time–frequency domain provided by a TFR. This is achieved by using a formulation often called "Time–Frequency Distribution", abbreviated as TFD.
TFRs are often complex-valued fields over time and frequency, where the modulus of the field represents "energy density" (the concentration of the root mean square
Root mean square
In mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids...
over time and frequency) or amplitude, and the argument of the field represents phase.
Background and motivation
A signalSignal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, as a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of time, may be considered as a representation with perfect time resolution.
In contrast, the magnitude
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
of the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
(FT) of the signal may be considered as a representation with perfect spectral resolution but with no time information because the magnitude of the FT conveys frequency content but it fails to convey when, in time, different events occur in the signal.
TFRs provide a bridge between these two representations in that they provide some temporal information and some spectral information simultaneously. Thus, TFRs are useful for the representation and analysis of signals containing multiple time-varying frequencies.
Quadratic forms
One form of TFR (or TFD) can be formulated by the multiplicative comparison of a signal with itself, expanded in different directions about each point in time. Such representations and formulations are known as quadraticQuadratic
In mathematics, the term quadratic describes something that pertains to squares, to the operation of squaring, to terms of the second degree, or equations or formulas that involve such terms...
TFRs or TFDs (QTFRs or QTFDs) because the representation is quadratic in the signal. This formulation was first described by Eugene Wigner in 1932 in the context of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and, later, reformulated as a general TFR by Ville in 1948 to form what is now known as the Wigner–Ville distribution, as it was shown in that Wigner's formula needed to use the anaytic signal defined in Ville's paper to be useful as a representation and for a practical analysis. Today, various QTFRs include but not limited to spectrogram
Spectrogram
A spectrogram is a time-varying spectral representation that shows how the spectral density of a signal varies with time. Also known as spectral waterfalls, sonograms, voiceprints, or voicegrams, spectrograms are used to identify phonetic sounds, to analyse the cries of animals; they were also...
(squared magnitude of short-time Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
), scaleogram
Scaleogram
In signal processing, a scaleogram or scalogram is a visual method of displaying a wavelet transform. There are 3 axes: x representing time, y representing scale, and z representing coefficient value. The z axis is often shown by varying the colour or brightness.A scaleogram is the equivalent of...
(squared magnitude of Wavelet transform) and the smoothed pseudo-Wigner distribution. In fact, a whole class of representations using bilinear time–frequency distributions fall in this category.
Although quadratic TFRs offer perfect temporal and spectral resolutions simultaneously, the quadratic nature of the transforms creates cross-terms. The following can be used to estimate which QTFRs contain cross terms.
Given a QTFR
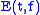defined on 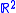, define a constant 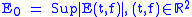and a set 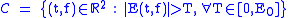. The QTFR, 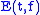is cross-term free if is a convex setConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
.
Linear forms
The cross-terms caused by the bilinear structure of TFDs and TFRs may be useful in some applications such as classification as the cross-terms provide extra detail for the recognition algorithm. However, in some other applications, these cross-terms may plague certain quadratic TFRs and they would need to be reduced. One way to do this is obtained by comparing the signal with a different function. Such resulting representations are known as linear TFRs because the representation is linear in the signal.The windowed Fourier transform (also known as the short-time Fourier transform
Short-time Fourier transform
The short-time Fourier transform , or alternatively short-term Fourier transform, is a Fourier-related transform used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time....
) localises the signal by modulating it with a window function, before performing the Fourier transform to obtain the frequency content of the signal in the region of the window.
Wavelet transforms
Wavelet transforms, in particular the continuous wavelet transformContinuous wavelet transform
A continuous wavelet transform is used to divide a continuous-time function into wavelets. Unlike Fourier transform, the continuous wavelet transform possesses the ability to construct a time-frequency representation of a signal that offers very good time and frequency localization...
, expand the signal in terms of wavelet functions which are localised in both time and frequency. Thus the wavelet transform of a signal may be represented in terms of both time and frequency.
The notions of time, frequency, and amplitude used to generate a TFR from a wavelet transform were originally developed intuitively. In 1992, Delprat et al. gave a quantitative derivation of these relationships, based upon a stationary phase approximation.
Linear canonical transformation
Linear canonical transformationLinear canonical transformation
In Hamiltonian mechanics, the linear canonical transformation is a family of integral transforms that generalizes many classical transforms...
s are the linear transforms of the time–frequency representation that preserve the symplectic form. These include and generalize the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
, fractional Fourier transform
Fractional Fourier transform
In mathematics, in the area of harmonic analysis, the fractional Fourier transform is a linear transformation generalizing the Fourier transform. It can be thought of as the Fourier transform to the n-th power where n need not be an integer — thus, it can transform a function to an...
, and others, thus providing a unified view of these transforms in terms of their action on the time–frequency domain.