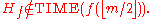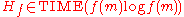Time hierarchy theorem
Encyclopedia
In computational complexity theory
, the time hierarchy theorems are important statements about time-bounded computation on Turing machine
s. Informally, these theorems say that given more time, a Turing machine can solve more problems. For example, there are problems that can be solved with n2 time but not n time.
The time hierarchy theorem for deterministic multi-tape Turing machines
was first proven by Richard Stearns
and Juris Hartmanis
in 1965. It was improved a year later when F. C. Hennie and Richard Stearns improved the efficiency of the Universal Turing machine. As a consequence, for every deterministic time-bounded complexity class
, there is a strictly larger time-bounded complexity class, and so the time-bounded hierarchy of complexity classes does not completely collapse. More precisely, the time hierarchy theorem for deterministic Turing machines states that for all time-constructible function
s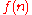
,
.
The time hierarchy theorem for nondeterministic Turing machines was originally proven by Stephen Cook
in 1972. It was improved to its current form via a complex proof by Joel Seiferas, Michael Fischer
, and Albert Meyer
in 1978. Finally in 1983, Stanislav Žák achieved the same result with the simple proof taught today. The time hierarchy theorem for nondeterministic Turing machines states that if g(n) is a time-constructible function, and f(n+1) = o(g(n)), then
.
The analogous theorems for space are the space hierarchy theorem
s. A similar theorem is not known for time-bounded probabilistic complexity classes, unless the class also has advice
.
. A function
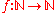is time-constructible if there exists a deterministic Turing machine
such that for every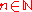
, if the machine is started with an input of n ones, it will halt after precisely 
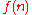steps. All polynomial
s with non-negative integral coefficients are time-constructible, as are exponential functions such as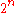
.
. We then show that the machine is in TIME(g(n)), using a simulator machine.
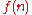is a time-constructible function, then there exists a decision problem
which cannot be solved in worst-case deterministic time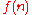
but can be solved in worst-case deterministic time 
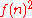. In other words, the complexity class DTIME
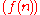is a strict subset of DTIME
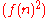. Note that 
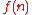is at least n, since smaller functions are never time-constructible.
Even more generally, it can be shown that if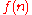
is time-constructible, then 
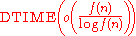is properly contained in 
. For example, there are problems solvable in time n2 but not time n, since n is in 
.
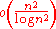To prove this, we first define a language as follows:
Here, M is a deterministic Turing machine, and x is its input (the initial contents of its tape). [M] denotes an input that encodes the Turing machine M. Let m be the size of the tuple ([M], x).
We know that we can decide membership of Hf by way of a deterministic Turing machine that first calculates f(|x|), then writes out a row of 0s of that length, and then uses this row of 0s as a "clock" or "counter" to simulate M for at most that many steps. At each step, the simulating machine needs to look through the definition of M to decide what the next action would be. It is safe to say that this takes at most f(m)3 operations, so
The rest of the proof will show that
so that if we substitute 2n + 1 for m, we get the desired result. Let us assume that Hf is in this time complexity class, and we will attempt to reach a contradiction.
If Hf is in this time complexity class, it means we can construct some machine K which, given some machine description [M] and input x, decides whether the tuple ([M], x) is in Hf within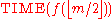
.
Therefore we can use this K to construct another machine, N, which takes a machine description [M] and runs K on the tuple ([M], [M]), and then accepts only if K rejects, and rejects if K accepts. If now n is the length of the input to N, then m (the length of the input to K) is twice n plus some delimiter symbol, so m = 2n + 1. N's running time is thus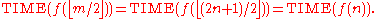
Now if we feed [N] as input into N itself (which makes n the length of [N]) and ask the question whether N accepts its own description as input, we get:
We thus conclude that the machine K does not exist, and so
It has been shown that a more efficient model of simulation exists which establishes that
but since this model of simulation is rather involved, it is not included here.
(g(n)), then there exists a decision problem which cannot be solved in non-deterministic time f(n) but can be solved in non-deterministic time g(n). In other words, the complexity class NTIME
(f(n)) is a strict subset of NTIME(g(n)).
⊂ EXPTIME
⊂ 2-EXP ⊂ ... and NP
⊂ NEXPTIME
⊂ 2-NEXP ⊂ ....
For example, P ⊂ EXPTIME since P ⊆ DTIME(2n) ⊂ DTIME(22n) ⊆ EXPTIME.
The theorem also guarantees that there are problems in P requiring arbitrary large exponents to solve; in other words, P does not collapse to DTIME(nk) for any fixed k. For example, there are problems solvable in n5000 time but not n4999 time. This is one argument against Cobham's thesis
, the convention that P is a practical class of algorithms. If such a collapse did occur, we could deduce that P ≠ PSPACE, since it is a well-known theorem that DTIME(f(n)) is strictly contained in DSPACE(f(n)).
However, the time hierarchy theorems provide no means to relate deterministic and non-deterministic complexity, or time and space complexity, so they cast no light on the great unsolved questions of computational complexity theory
: whether P and NP, NP and PSPACE
, PSPACE and EXPTIME, or EXPTIME and NEXPTIME are equal or not.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, the time hierarchy theorems are important statements about time-bounded computation on Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
s. Informally, these theorems say that given more time, a Turing machine can solve more problems. For example, there are problems that can be solved with n2 time but not n time.
The time hierarchy theorem for deterministic multi-tape Turing machines
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
was first proven by Richard Stearns
Richard Stearns (computer scientist)
Richard Edwin Stearns is a prominent computer scientist who, with Juris Hartmanis, received the 1993 ACM Turing Award "in recognition of their seminal paper which established the foundations for the field of computational complexity theory"...
and Juris Hartmanis
Juris Hartmanis
Juris Hartmanis is a prominent computer scientist and computational theorist who, with Richard E. Stearns, received the 1993 ACM Turing Award "in recognition of their seminal paper which established the foundations for the field of computational complexity theory".Hartmanis was born in Latvia...
in 1965. It was improved a year later when F. C. Hennie and Richard Stearns improved the efficiency of the Universal Turing machine. As a consequence, for every deterministic time-bounded complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
, there is a strictly larger time-bounded complexity class, and so the time-bounded hierarchy of complexity classes does not completely collapse. More precisely, the time hierarchy theorem for deterministic Turing machines states that for all time-constructible function
Constructible function
In complexity theory, a time-constructible function is a function f from natural numbers to natural numbers with the property that f can be constructed from n by a Turing machine in the time of order f...
s
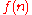,.The time hierarchy theorem for nondeterministic Turing machines was originally proven by Stephen Cook
Stephen Cook
Stephen Arthur Cook is a renowned American-Canadian computer scientist and mathematician who has made major contributions to the fields of complexity theory and proof complexity...
in 1972. It was improved to its current form via a complex proof by Joel Seiferas, Michael Fischer
Michael J. Fischer
Michael John Fischer is a computer scientist who works in the fields of distributed computing, parallel computing, cryptography, algorithms and data structures, and computational complexity.-Career:...
, and Albert Meyer
Albert R. Meyer
Albert Ronald da Silva Meyer is a professor of computer science at Massachusetts Institute of Technology . He has been a Fellow of the American Academy of Arts and Sciences since 1987, and he was inducted as a Fellow of the Association for Computing Machinery in 2000.Meyer's seminal works...
in 1978. Finally in 1983, Stanislav Žák achieved the same result with the simple proof taught today. The time hierarchy theorem for nondeterministic Turing machines states that if g(n) is a time-constructible function, and f(n+1) = o(g(n)), then
.The analogous theorems for space are the space hierarchy theorem
Space hierarchy theorem
In computational complexity theory, the space hierarchy theorems are separation results that show that both deterministic and nondeterministic machines can solve more problems in more space, subject to certain conditions. For example, a deterministic Turing machine can solve more decision problems...
s. A similar theorem is not known for time-bounded probabilistic complexity classes, unless the class also has advice
Advice (complexity)
In computational complexity theory, an advice string is an extra input to a Turing machine which is allowed to depend on the length n of the input, but not on input itself...
.
Background
Both theorems use the notion of a time-constructible functionConstructible function
In complexity theory, a time-constructible function is a function f from natural numbers to natural numbers with the property that f can be constructed from n by a Turing machine in the time of order f...
. A function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
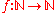is time-constructible if there exists a deterministic Turing machineTuring machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
such that for every
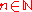, if the machine is started with an input of n ones, it will halt after precisely 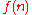steps. All polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s with non-negative integral coefficients are time-constructible, as are exponential functions such as
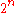.Proof overview
We need to prove that some time class TIME(g(n)) is strictly larger than some time class TIME(f(n)). We do this by constructing a machine which cannot be in TIME(f(n)), by diagonalizationCantor's diagonal argument
Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
. We then show that the machine is in TIME(g(n)), using a simulator machine.
Statement
The theorem states that: If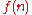 is a time-constructible function, then there exists a decision problemDecision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
which cannot be solved in worst-case deterministic time
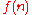but can be solved in worst-case deterministic time 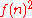. In other words, the complexity class DTIMEDTIME
In computational complexity theory, DTIME is the computational resource of computation time for a deterministic Turing machine. It represents the amount of time that a "normal" physical computer would take to solve a certain computational problem using a certain algorithm...
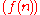is a strict subset of DTIME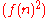. Note that 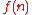is at least n, since smaller functions are never time-constructible.Even more generally, it can be shown that if
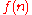is time-constructible, then 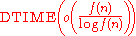is properly contained in . For example, there are problems solvable in time n2 but not time n, since n is in 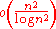.Proof
We include here a proof that DTIME(f(n)) is a strict subset of DTIME(f(2n + 1)3) as it is simpler. See the bottom of this section for information on how to extend the proof to f(n)2.To prove this, we first define a language as follows:
Here, M is a deterministic Turing machine, and x is its input (the initial contents of its tape). [M] denotes an input that encodes the Turing machine M. Let m be the size of the tuple ([M], x).
We know that we can decide membership of Hf by way of a deterministic Turing machine that first calculates f(|x|), then writes out a row of 0s of that length, and then uses this row of 0s as a "clock" or "counter" to simulate M for at most that many steps. At each step, the simulating machine needs to look through the definition of M to decide what the next action would be. It is safe to say that this takes at most f(m)3 operations, so
The rest of the proof will show that
so that if we substitute 2n + 1 for m, we get the desired result. Let us assume that Hf is in this time complexity class, and we will attempt to reach a contradiction.
If Hf is in this time complexity class, it means we can construct some machine K which, given some machine description [M] and input x, decides whether the tuple ([M], x) is in Hf within
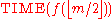.Therefore we can use this K to construct another machine, N, which takes a machine description [M] and runs K on the tuple ([M], [M]), and then accepts only if K rejects, and rejects if K accepts. If now n is the length of the input to N, then m (the length of the input to K) is twice n plus some delimiter symbol, so m = 2n + 1. N's running time is thus
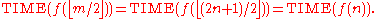
Now if we feed [N] as input into N itself (which makes n the length of [N]) and ask the question whether N accepts its own description as input, we get:
- If N accepts [N] (which we know it does in at most f(n) operations), this means that K rejects ([N], [N]), so ([N], [N]) is not in Hf, and thus N does not accept [N] in f(n) steps. Contradiction!
- If N rejects [N] (which we know it does in at most f(n) operations), this means that K accepts ([N], [N]), so ([N], [N]) is in Hf, and thus N does accept [N] in f(n) steps. Contradiction!
We thus conclude that the machine K does not exist, and so
Extension
The reader may have realised that the proof is simpler because we have chosen a simple Turing machine simulation for which we can be certain that
It has been shown that a more efficient model of simulation exists which establishes that
but since this model of simulation is rather involved, it is not included here.
Non-deterministic time hierarchy theorem
If g(n) is a time-constructible function, and f(n+1) = oBig O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(g(n)), then there exists a decision problem which cannot be solved in non-deterministic time f(n) but can be solved in non-deterministic time g(n). In other words, the complexity class NTIME
NTIME
In computational complexity theory, the complexity class NTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time O, and unlimited space....
(f(n)) is a strict subset of NTIME(g(n)).
Consequences
The time hierarchy theorems guarantee that the deterministic and non-deterministic versions of the exponential hierarchy are genuine hierarchies: in other words PP (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
⊂ EXPTIME
EXPTIME
In computational complexity theory, the complexity class EXPTIME is the set of all decision problems solvable by a deterministic Turing machine in O time, where p is a polynomial function of n....
⊂ 2-EXP ⊂ ... and NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
⊂ NEXPTIME
NEXPTIME
In computational complexity theory, the complexity class NEXPTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time O for some polynomial p, and unlimited space....
⊂ 2-NEXP ⊂ ....
For example, P ⊂ EXPTIME since P ⊆ DTIME(2n) ⊂ DTIME(22n) ⊆ EXPTIME.
The theorem also guarantees that there are problems in P requiring arbitrary large exponents to solve; in other words, P does not collapse to DTIME(nk) for any fixed k. For example, there are problems solvable in n5000 time but not n4999 time. This is one argument against Cobham's thesis
Cobham's Thesis
Cobham's thesis, also known as Cobham–Edmonds thesis , asserts that computational problems can be feasibly computed on some computational device only if they can be computed in polynomial time; that is, if they lie in the complexity class P.Formally, to say that a problem can be solved in...
, the convention that P is a practical class of algorithms. If such a collapse did occur, we could deduce that P ≠ PSPACE, since it is a well-known theorem that DTIME(f(n)) is strictly contained in DSPACE(f(n)).
However, the time hierarchy theorems provide no means to relate deterministic and non-deterministic complexity, or time and space complexity, so they cast no light on the great unsolved questions of computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
: whether P and NP, NP and PSPACE
PSPACE
In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :...
, PSPACE and EXPTIME, or EXPTIME and NEXPTIME are equal or not.