
Toda field theory
Encyclopedia
In the study of field theory and partial differential equation
s, a Toda field theory (named after Morikazu Toda) is derived from the following Lagrangian
:
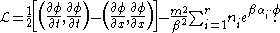
Here x and t are spacetime coordinates, is the Killing form
of a real r-dimensional Cartan algebra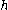 of a Kac-Moody algebra over
of a Kac-Moody algebra over 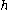 , αi is the ith simple root
, αi is the ith simple root
in some root basis, ni is the Coxeter number
, m is the mass (or bare mass in the quantum field theory
version) and β is the coupling constant.
Then a Toda field theory is the study of a function φ mapping 2 dimensional Minkowski space
satisfying the corresponding Euler-Lagrange equation
s.
If the Kac-Moody algebra is finite, it's called a Toda field theory. If it is affine, it is called an affine Toda field theory (after the component of φ which decouples is removed) and if it is hyperbolic, it is called a hyperbolic Toda field theory.
Toda field theories are integrable models and their solutions describe soliton
s.
The sinh-Gordon model is the affine Toda field theory with the generalized Cartan matrix
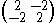
and a positive value for β after we project out a component of φ which decouples.
The sine-Gordon model is the model with the same Cartan matrix but an imaginary β.
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s, a Toda field theory (named after Morikazu Toda) is derived from the following Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
:
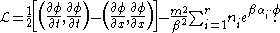
Here x and t are spacetime coordinates, is the Killing form
Killing form
In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
of a real r-dimensional Cartan algebra
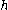 of a Kac-Moody algebra over
of a Kac-Moody algebra over  , αi is the ith simple root
, αi is the ith simple rootSimple root
in mathematics the term simple root can refer to one of two unrelated notions:*A simple root of a polynomial is a root of multiplicity one*A simple root in a root system is a member of a subset determined by a choice of positive roots...
in some root basis, ni is the Coxeter number
Coxeter number
In mathematics, the Coxeter number h is the order of a Coxeter element of an irreducible Coxeter group, hence also of a root system or its Weyl group. It is named after H.S.M. Coxeter.-Definitions:...
, m is the mass (or bare mass in the quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
version) and β is the coupling constant.
Then a Toda field theory is the study of a function φ mapping 2 dimensional Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
satisfying the corresponding Euler-Lagrange equation
Euler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
s.
If the Kac-Moody algebra is finite, it's called a Toda field theory. If it is affine, it is called an affine Toda field theory (after the component of φ which decouples is removed) and if it is hyperbolic, it is called a hyperbolic Toda field theory.
Toda field theories are integrable models and their solutions describe soliton
Soliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
s.
The sinh-Gordon model is the affine Toda field theory with the generalized Cartan matrix
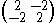
and a positive value for β after we project out a component of φ which decouples.
The sine-Gordon model is the model with the same Cartan matrix but an imaginary β.

