
Tonelli's theorem (functional analysis)
Encyclopedia
In mathematics
, Tonelli's theorem in functional analysis is a fundamental result on the weak
lower semicontinuity of nonlinear functionals
on Lp spaces
. As such, it has major implications for functional analysis
and the calculus of variations
. Roughly, it shows that weak lower semicontinuity for integral functionals is equivalent to convexity
of the integral kernel. The result is attributed to the Italian
mathematician
Leonida Tonelli
.
domain
in n-dimension
al Euclidean space
Rn and let f : Rm → R ∪ {±∞} be a continuous
extended real-valued
function. Define a nonlinear functional F on functions u : Ω → Rm by
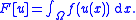
Then F is sequentially weakly lower semicontinuous on the Lp space Lp(Ω; Rm) for 1 < p < +∞ and weakly-∗ lower semicontinuous on L∞(Ω; Rm) if and only if
the function f

is convex.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Tonelli's theorem in functional analysis is a fundamental result on the weak
Weak topology
In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
lower semicontinuity of nonlinear functionals
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
on Lp spaces
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
. As such, it has major implications for functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
. Roughly, it shows that weak lower semicontinuity for integral functionals is equivalent to convexity
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
of the integral kernel. The result is attributed to the Italian
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Leonida Tonelli
Leonida Tonelli
Leonida Tonelli was an Italian mathematician, most noted for creating Tonelli's theorem, usually considered a forerunner to Fubini's theorem.-External links:...
.
Statement of the theorem
Let Ω be an openOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
domain
Domain (ring theory)
In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
in n-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn and let f : Rm → R ∪ {±∞} be a continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
extended real-valued
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
function. Define a nonlinear functional F on functions u : Ω → Rm by
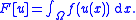
Then F is sequentially weakly lower semicontinuous on the Lp space Lp(Ω; Rm) for 1 < p < +∞ and weakly-∗ lower semicontinuous on L∞(Ω; Rm) if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the function f

is convex.

