
Topological pair
Encyclopedia
In mathematics
, more specifically algebraic topology
, a pair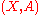 is short-hand for an inclusion of topological spaces
is short-hand for an inclusion of topological spaces  . Sometimes
. Sometimes 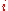 is assumed to be a cofibration
is assumed to be a cofibration
. A morphism from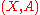 to
to 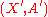 is given by two maps
is given by two maps 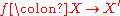 and
and
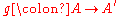 such that
such that 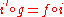 .
.
Pairs come up mainly in homology theory
and cohomology theory, where chains in are made equivalent to 0, when considered as chains in
are made equivalent to 0, when considered as chains in  .
.
Heuristically, one often thinks of a pair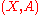 as being akin to the quotient space
as being akin to the quotient space  .
.
There is a functor from spaces to pairs, which sends a space to the pair
to the pair  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, a pair
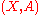 is short-hand for an inclusion of topological spaces
is short-hand for an inclusion of topological spaces  . Sometimes
. Sometimes 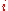 is assumed to be a cofibration
is assumed to be a cofibrationCofibration
In mathematics, in particular homotopy theory, a continuous mappingi\colon A \to X,where A and X are topological spaces, is a cofibration if it satisfies the homotopy extension property with respect to all spaces Y. The name is because the dual condition, the homotopy lifting property, defines...
. A morphism from
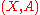 to
to 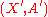 is given by two maps
is given by two maps 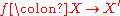 and
and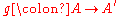 such that
such that 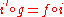 .
.Pairs come up mainly in homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
and cohomology theory, where chains in
 are made equivalent to 0, when considered as chains in
are made equivalent to 0, when considered as chains in  .
.Heuristically, one often thinks of a pair
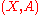 as being akin to the quotient space
as being akin to the quotient space  .
.There is a functor from spaces to pairs, which sends a space
 to the pair
to the pair  .
.

