Tortuosity is a property of curve

Curve

In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...

 being tortuous (twisted; having many turns). There have been several attempts to quantify this property. Tortuosity is commonly used to describe diffusion

Diffusion

Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...

 in porous media . This concept is also used for porous media, such as soils and snow .

Tortuosity in 2-D

Subjective estimation (sometimes aided by optometric grading scales) is often used.

The most simple mathematic method to estimate tortuosity is arc-chord ratio: ratio of the length

Arc length

Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...

 of the curve (L) to the distance between the ends of it (C):


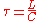
Arc-chord ratio equals 1 for a straight line and is infinite for a circle.

Another method, proposed in 1999, is to estimate the tortuosity as integral

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

 of square (or module) of curvature

Curvature

In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...

. Dividing the result by length of curve or chord has also been tried.

In 2002 several Italian scientists proposed one more method. At first, the curve is divided into several (N) parts with constant sign of curvature (using hysteresis

Hysteresis

Hysteresis is the dependence of a system not just on its current environment but also on its past. This dependence arises because the system can be in more than one internal state. To predict its future evolution, either its internal state or its history must be known. If a given input alternately...

 to decrease sensitivity to noise). Then the arc-chord ratio for each part is found and the tortuosity is estimated by:


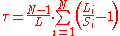
In this case tortuosity of both straight line and circle is estimated to be 0.

In 1993 Swiss mathematician Martin Mächler proposed an analogy: it’s relatively easy to drive a bicycle or a car in a trajectory with a constant curvature (an arc of a circle), but it’s much harder to drive where curvature changes. This would imply that roughness (or tortuosity) could be measured by relative change of curvature. In this case the proposed "local" measure was derivative

Derivative

In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...

 of logarithm

Logarithm

The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...

 of curvature:


However, in this case tortuosity of a straight line is left undefined.

In 2005 it was proposed to measure tortuosity by an integral of square of derivative of curvature, divided by the length of a curve:


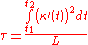
In this case tortuosity of both straight line and circle is estimated to be 0.

In most of these methods digital filters and approximation

Approximation

An approximation is a representation of something that is not exact, but still close enough to be useful. Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws.Approximations may be used because...

 by splines can be used to decrease sensitivity to noise.

Tortuosity in 3-D

Usually subjective estimation is used. However, several ways to adapt methods estimating tortuosity in 2-D have also been tried. The methods include arc-chord ratio, arc-chord ratio divided by number of inflection point

Inflection point

In differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa...

s and integral of square of curvature, divided by length of the curve (curvature is estimated assuming that small segments of curve are planar) . Another method used for quantifying tortuosity in 3D has been applied in 3D reconstructions of solid oxide fuel cell cathodes where the Euclidean distance sums of the centroids of a pore were divided by the length of the pore.

Applications of tortuosity

Tortuosity of blood vessels (for example, retinal

Retina

The vertebrate retina is a light-sensitive tissue lining the inner surface of the eye. The optics of the eye create an image of the visual world on the retina, which serves much the same function as the film in a camera. Light striking the retina initiates a cascade of chemical and electrical...

 and cerebral

Brain

The brain is the center of the nervous system in all vertebrate and most invertebrate animals—only a few primitive invertebrates such as sponges, jellyfish, sea squirts and starfishes do not have one. It is located in the head, usually close to primary sensory apparatus such as vision, hearing,...

 blood vessels) is known to be used as a medical sign

Medical sign

A medical sign is an objective indication of some medical fact or characteristic that may be detected by a physician during a physical examination of a patient....

.

In mathematics, cubic splines minimize the functional

Functional

Generally, functional refers to something able to fulfill its purpose or function.*Functionalism and Functional form, movements in architectural design*Functional group, certain atomic combinations that occur in various molecules, e.g...

, equivalent to integral of square of curvature (approximating the curvature as the second derivative).

In many engineering domains dealing with mass transfer in porous materials, such as hydrogeology

Hydrogeology

Hydrogeology is the area of geology that deals with the distribution and movement of groundwater in the soil and rocks of the Earth's crust, . The term geohydrology is often used interchangeably...

 or heterogeneous catalysis

Heterogeneous catalysis

In chemistry, heterogeneous catalysis refers to the form of catalysis where the phase of the catalyst differs from that of the reactants. Phase here refers not only to solid, liquid, vs gas, but also immiscible liquids, e.g. oil and water. The great majority of practical heterogeneous catalysts...

, the tortuosity refers to the ratio of the diffusivity in the free space to the diffusivity in the porous medium

Porous medium

A porous medium is a material containing pores . The skeletal portion of the material is often called the "matrix" or "frame". The pores are typically filled with a fluid...

 (analogous to arc-chord ratio of path). Strictly speaking, however, the effective diffusivity is proportional to the reciprocal of the square of the geometrical tortuosity

In acoustics

Acoustics

Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...

 and following initial works by Maurice Anthony Biot

Maurice Anthony Biot

Maurice Anthony Biot was a Belgian-American physicist and the founder of the theory of poroelasticity.Born in Antwerp, Belgium, Biot studied at Catholic University of Leuven in Belgium where he received a bachelor's degrees in philosophy , mining engineering and electrical engineering , and...

 in 1956, the tortuosity is used to describe sound propagation in fluid-saturated porous media. In such media, when frequency of the sound wave is high enough, the effect of viscous drag force between the solid and the fluid can be ignored. In this case, velocity of sound propagation in the fluid in the pores is non-dispersive and compared with the value of the velocity of sound in the free fluid is reduced by a ratio equal to the square root of the tortuosity. This has been used for a number of applications including the study of materials for acoustic isolation, and for oil prospection using acoustics means.

In analytical chemistry

Analytical chemistry

Analytical chemistry is the study of the separation, identification, and quantification of the chemical components of natural and artificial materials. Qualitative analysis gives an indication of the identity of the chemical species in the sample and quantitative analysis determines the amount of...

 applied to polymer

Polymer

A polymer is a large molecule composed of repeating structural units. These subunits are typically connected by covalent chemical bonds...

s and sometimes small molecules tortuosity is applied in Gel permeation chromatography

Gel Permeation Chromatography

Gel permeation chromatography is a type of size exclusion chromatography , that separates analytes on the basis of size. The technique is often used for the analysis of polymers. As a technique, SEC was first developed in 1955 by Lathe and Ruthven. The term gel permeation chromatography can be...

 (GPC) also known as Size Exclusion Chromatography (SEC). As with any chromatography

Chromatography

Chromatography is the collective term for a set of laboratory techniques for the separation of mixtures....

 it is used to separate mixture

Mixture

In chemistry, a mixture is a material system made up by two or more different substances which are mixed together but are not combined chemically...

s. In the case of GPC the separation is based on molecular size and it works by the use of stationary media with appropriately dimensioned pores. The separation occurs because larger molecules take a shorter, less tortuous path and elute more quickly and smaller molecules can pass into the pores and take a longer, more tortuous path and elute later.