
Total functional programming
Encyclopedia
Total functional programming (also known as strong functional programming, to be contrasted with ordinary, or weak functional programming
) is a programming
paradigm that restricts the range of programs to those that are provably terminating
.
Termination is guaranteed through a restricted form of recursion
, which operates only upon ‘reduced’ forms of its arguments. One such form is Walther recursion
. In addition, every function must be a total (as opposed to partial
) function. That is, it must have a definition for everything inside its domain. This may lead to unexpected or arbitrary definitions such as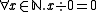
These restrictions mean that total functional programming is not Turing-complete. However, the set of algorithms that can be used is still huge. For example, any algorithm that has had an asymptotic upper bound
calculated for it can be trivially transformed into a provably-terminating function by using the upper bound as an extra argument decremented on each iteration or recursion.
Another outcome of total functional programming is that both strict evaluation and lazy evaluation
result in the same behaviour, in principle; however, one or the other may still be preferable (or even required) for performance reasons.
Total functional programming must necessarily also make a distinction between data
and codata—the former is finitary
, while the latter is potentially infinite. Such potentially infinite data structures are needed for applications such as I/O
. Using codata entails the usage of such operations as corecursion
.
Both Epigram and Charity could be considered total functional programming languages, even though they don't work in the way Turner specifies in his paper. So could programming directly in plain System F
, in Martin-Löf type theory or the Calculus of Constructions
.
Functional programming
In computer science, functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids state and mutable data. It emphasizes the application of functions, in contrast to the imperative programming style, which emphasizes changes in state...
) is a programming
Computer programming
Computer programming is the process of designing, writing, testing, debugging, and maintaining the source code of computer programs. This source code is written in one or more programming languages. The purpose of programming is to create a program that performs specific operations or exhibits a...
paradigm that restricts the range of programs to those that are provably terminating
Machine that always halts
In computability theory, a machine that always halts—also called a decider or a total Turing machine —is a Turing machine that halts for every input....
.
Termination is guaranteed through a restricted form of recursion
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
, which operates only upon ‘reduced’ forms of its arguments. One such form is Walther recursion
Walther recursion
In computer programming, Walther recursion is a method of analysing recursive functions that can determine if the function is definitely terminating, given finite inputs...
. In addition, every function must be a total (as opposed to partial
Partial function
In mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function...
) function. That is, it must have a definition for everything inside its domain. This may lead to unexpected or arbitrary definitions such as
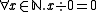
These restrictions mean that total functional programming is not Turing-complete. However, the set of algorithms that can be used is still huge. For example, any algorithm that has had an asymptotic upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
calculated for it can be trivially transformed into a provably-terminating function by using the upper bound as an extra argument decremented on each iteration or recursion.
Another outcome of total functional programming is that both strict evaluation and lazy evaluation
Lazy evaluation
In programming language theory, lazy evaluation or call-by-need is an evaluation strategy which delays the evaluation of an expression until the value of this is actually required and which also avoids repeated evaluations...
result in the same behaviour, in principle; however, one or the other may still be preferable (or even required) for performance reasons.
Total functional programming must necessarily also make a distinction between data
Data
The term data refers to qualitative or quantitative attributes of a variable or set of variables. Data are typically the results of measurements and can be the basis of graphs, images, or observations of a set of variables. Data are often viewed as the lowest level of abstraction from which...
and codata—the former is finitary
Finitary
In mathematics or logic, a finitary operation is one, like those of arithmetic, that takes a finite number of input values to produce an output. An operation such as taking an integral of a function, in calculus, is defined in such a way as to depend on all the values of the function , and is so...
, while the latter is potentially infinite. Such potentially infinite data structures are needed for applications such as I/O
I/O
I/O may refer to:* Input/output, a system of communication for information processing systems* Input-output model, an economic model of flow prediction between sectors...
. Using codata entails the usage of such operations as corecursion
Corecursion
In computer science, corecursion is a type of operation that is dual to recursion. Corecursion and codata allow total languages to work with infinite data structures such as streams. Corecursion is often used in conjunction with lazy evaluation. Corecursion can produce both finite and infinite data...
.
Both Epigram and Charity could be considered total functional programming languages, even though they don't work in the way Turner specifies in his paper. So could programming directly in plain System F
System F
System F, also known as the polymorphic lambda calculus or the second-order lambda calculus, is a typed lambda calculus that differs from the simply typed lambda calculus by the introduction of a mechanism of universal quantification over types...
, in Martin-Löf type theory or the Calculus of Constructions
Calculus of constructions
The calculus of constructions is a formal language in which both computer programs and mathematical proofs can be expressed. This language forms the basis of theory behind the Coq proof assistant, which implements the derivative calculus of inductive constructions.-General traits:The CoC is a...
.

