
Total sum of squares
Encyclopedia
In statistical data analysis
the total sum of squares (TSS) is a quantity that appears as part of a standard way of presenting results of such analyses. It is defined as being the sum, over all observations, of the squared differences of each observation from the overall mean
.
In statistical
linear model
s, (particularly in standard regression models), the TSS is the sum
of the squares of the difference of the dependent variable and its grand mean
:
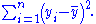
For wide classes of linear models:
Total sum of squares = explained sum of squares
+ residual sum of squares
. For a proof of this in the multivariate OLS case, see partitioning in the general OLS model.
In analysis of variance
(ANOVA) the total sum of squares is the sum of the so-called "within-samples" sum of squares and "between-samples" sum of squares, i.e., partitioning of the sum of squares.
In multivariate analysis of variance (MANOVA) the following equation applies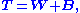
where T is the total sum of squares and products (SSP) matrix
, W is the within-samples SSP matrix and B is the between-samples SSP matrix.
Similar terminology may also be used in linear discriminant analysis
, where W and B are respectively referred to as the within-groups and between-groups SSP matrics.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
the total sum of squares (TSS) is a quantity that appears as part of a standard way of presenting results of such analyses. It is defined as being the sum, over all observations, of the squared differences of each observation from the overall mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
.
In statistical
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
linear model
Linear model
In statistics, the term linear model is used in different ways according to the context. The most common occurrence is in connection with regression models and the term is often taken as synonymous with linear regression model. However the term is also used in time series analysis with a different...
s, (particularly in standard regression models), the TSS is the sum
SUM
SUM can refer to:* The State University of Management* Soccer United Marketing* Society for the Establishment of Useful Manufactures* StartUp-Manager* Software User’s Manual,as from DOD-STD-2 167A, and MIL-STD-498...
of the squares of the difference of the dependent variable and its grand mean
Grand mean
The grand mean is the mean of the means of several subsamples. For example, consider several lots, each containing several items. The items from each lot are sampled for a measure of some variable and the means of the measurements from each lot are computed. The mean of the measures from each lot...
:
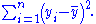
For wide classes of linear models:
Total sum of squares = explained sum of squares
Explained sum of squares
In statistics, the explained sum of squares is a quantity used in describing how well a model, often a regression model, represents the data being modelled...
+ residual sum of squares
Residual sum of squares
In statistics, the residual sum of squares is the sum of squares of residuals. It is also known as the sum of squared residuals or the sum of squared errors of prediction . It is a measure of the discrepancy between the data and an estimation model...
. For a proof of this in the multivariate OLS case, see partitioning in the general OLS model.
In analysis of variance
Analysis of variance
In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
(ANOVA) the total sum of squares is the sum of the so-called "within-samples" sum of squares and "between-samples" sum of squares, i.e., partitioning of the sum of squares.
In multivariate analysis of variance (MANOVA) the following equation applies
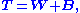
where T is the total sum of squares and products (SSP) matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, W is the within-samples SSP matrix and B is the between-samples SSP matrix.
Similar terminology may also be used in linear discriminant analysis
Linear discriminant analysis
Linear discriminant analysis and the related Fisher's linear discriminant are methods used in statistics, pattern recognition and machine learning to find a linear combination of features which characterizes or separates two or more classes of objects or events...
, where W and B are respectively referred to as the within-groups and between-groups SSP matrics.

