
Totally disconnected group
Encyclopedia
In mathematics
, a totally disconnected group is a topological group
that is totally disconnected. Such topological groups are necessarily Hausdorff
.
Interest centres on locally compact totally disconnected groups (variously referred to as groups of td-type, locally profinite groups, t.d. groups). The compact
case has been heavily studied – these are the profinite groups – but for a long time not much was known about the general case. A theorem of van Dantzig
from the 1930s, stating that every such group contains a compact open
subgroup
, was all that was known. Then groundbreaking work on this subject was done in 1994, when George Willis showed that every locally compact totally disconnected group contains a so-called tidy subgroup and a special function on its automorphisms, the scale function.
of the identity contains a compact open subgroup. Conversely, if a group is such that the identity has a neighbourhood basis consisting of compact open subgroups, then it is locally compact and totally disconnected.
 a continuous automorphism of G.
a continuous automorphism of G.
Define:
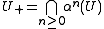
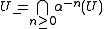
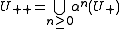
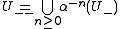
U is said to be tidy for if and only if
if and only if 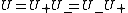 and
and 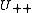 and
and  are closed.
are closed.
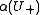 in
in 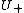 is shown to be finite and independent of the U which is tidy for
is shown to be finite and independent of the U which is tidy for  . Define the scale function
. Define the scale function 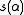 as this index. Restriction to inner automorphism
as this index. Restriction to inner automorphism
s gives a function on G with interesting properties. These are in particular:
Define the function on G by
on G by
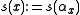 ,
,
where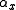 is the inner automorphism of
is the inner automorphism of  on G.
on G.
 is continuous.
is continuous.
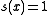 , whenever x in G is a compact element.
, whenever x in G is a compact element.
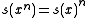 for every integer
for every integer  .
.
The modular function on G is given by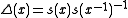 .
.
s and linear groups over local skew fields by Helge Glöckner.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a totally disconnected group is a topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
that is totally disconnected. Such topological groups are necessarily Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
.
Interest centres on locally compact totally disconnected groups (variously referred to as groups of td-type, locally profinite groups, t.d. groups). The compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
case has been heavily studied – these are the profinite groups – but for a long time not much was known about the general case. A theorem of van Dantzig
David van Dantzig
David van Dantzig was a Dutch mathematician, well known for the construction in topology of the dyadic solenoid....
from the 1930s, stating that every such group contains a compact open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
, was all that was known. Then groundbreaking work on this subject was done in 1994, when George Willis showed that every locally compact totally disconnected group contains a so-called tidy subgroup and a special function on its automorphisms, the scale function.
Locally compact case
In a locally compact, totally disconnected group, every neighbourhoodNeighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
of the identity contains a compact open subgroup. Conversely, if a group is such that the identity has a neighbourhood basis consisting of compact open subgroups, then it is locally compact and totally disconnected.
Tidy subgroups
Let G be a locally compact, totally disconnected group, U a compact open subgroup of G and a continuous automorphism of G.
a continuous automorphism of G.Define:
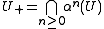
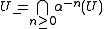
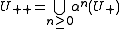
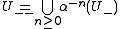
U is said to be tidy for
 if and only if
if and only if 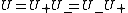 and
and 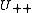 and
and  are closed.
are closed.The scale function
The index of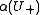 in
in 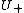 is shown to be finite and independent of the U which is tidy for
is shown to be finite and independent of the U which is tidy for  . Define the scale function
. Define the scale function 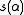 as this index. Restriction to inner automorphism
as this index. Restriction to inner automorphismInner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
s gives a function on G with interesting properties. These are in particular:
Define the function
 on G by
on G by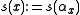 ,
,where
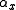 is the inner automorphism of
is the inner automorphism of  on G.
on G. is continuous.
is continuous.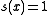 , whenever x in G is a compact element.
, whenever x in G is a compact element.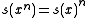 for every integer
for every integer  .
.The modular function on G is given by
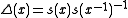 .
.Calculations and applications
The scale function was used to prove a conjecture by Hofmann and Mukherja and has been explicitly calculated for p-adic Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s and linear groups over local skew fields by Helge Glöckner.

