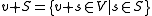In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a measure

Measure (mathematics)

In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...

 on a real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

 vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

 is said to be transverse to a given set if it assigns measure zero to every translate

Translation (geometry)

In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...

 of that set, while assigning finite and positive (i.e. non-zero) measure to some compact set

Compact space

In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

.

Definition

Let V be a real vector space together with a metric space

Metric space

In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...

 structure with respect to which it is a complete space

Complete space

In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....

. A Borel measure μ is said to be transverse to a Borel-measurable subset S of V if

• there exists a compact subset K of V with 0 < μ(K) < +∞; and
• μ(v + S) = 0 for all v ∈ V, where

is the translate of S by v.

The first requirement ensures that, for example, the trivial measure

Trivial measure

In mathematics, specifically in measure theory, the trivial measure on any measurable space is the measure μ which assigns zero measure to every measurable set: μ = 0 for all A in Σ.-Properties of the trivial measure:...

 is not considered to be a transverse measure.

Example

As an example, take V to be the Euclidean plane R² with its usual Euclidean norm/metric structure. Define a measure μ on R² by setting μ(E) to be the one-dimensional Lebesgue measure

Lebesgue measure

In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...

 of the intersection of E with the first coordinate axis:


An example of a compact set K with positive and finite μ-measure is K = B₁(0), the closed unit ball about the origin, which has μ(K) = 2. Now take the set S to be the second coordinate axis. Any translate (v₁, v₂) + S of S will meet the first coordinate axis in precisely one point, (v₁, 0). Since a single point has Lebesgue measure zero, μ((v₁, v₂) + S) = 0, and so μ is transverse to S.