
Tukey's test of additivity
Encyclopedia
In statistics
, Tukey's test of additivity, named for John Tukey
, is an approach used in two-way anova (regression analysis
involving two qualitative factors) to assess whether the factor variables are additively related to the expected value
of the response variable. It can be applied when there are no replicated values in the data set, a situation in which it is impossible to directly estimate a fully general non-additive regression structure and still have information left to estimate the error variance. The test statistic
proposed by Tukey has one degree of freedom under the null hypothesis, hence this is often called "Tukey's one-degree-of-freedom test."
(ANOVA) with one observation per cell. The response variable Yij is observed in a table of cells with the rows indexed by i = 1,..., m and the columns indexed by j = 1,..., n. The rows and columns typically correspond to various types and levels of treatment that are applied in combination.
The additive model states that the expected response can be expressed EYij = μ + αi + βj, where the αi and βj are unknown constant values. The unknown model parameters are usually estimated as


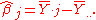
where Yi• is the mean of the ith row of the data table, Y•j is the mean of the jth column of the data table, and Y•• is the overall mean of the data table.
The additive model can be generalized to allow for arbitrary interaction effects by setting EYij = μ + αi + βj + γij. However after fitting the natural estimator of γij,
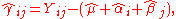
the fitted values

fit the data exactly. Thus there are no remaining degrees of freedom to estimate the variance σ2, and no hypothesis tests about the γij can performed.
Tukey therefore proposed a more constrained interaction model of the form
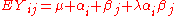
By testing the null hypothesis that λ = 0, we are able to detect some departures from additivity based only on the single parameter λ. To carry out the test, set
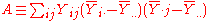

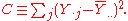
Then use the following test statistic

Under the null hypothesis, the test statistic has a F distribution with 1, q degrees of freedom, where q = mn − (m + n) is the degrees of freedom for estimating σ2.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, Tukey's test of additivity, named for John Tukey
John Tukey
John Wilder Tukey ForMemRS was an American statistician.- Biography :Tukey was born in New Bedford, Massachusetts in 1915, and obtained a B.A. in 1936 and M.Sc. in 1937, in chemistry, from Brown University, before moving to Princeton University where he received a Ph.D...
, is an approach used in two-way anova (regression analysis
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
involving two qualitative factors) to assess whether the factor variables are additively related to the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of the response variable. It can be applied when there are no replicated values in the data set, a situation in which it is impossible to directly estimate a fully general non-additive regression structure and still have information left to estimate the error variance. The test statistic
Test statistic
In statistical hypothesis testing, a hypothesis test is typically specified in terms of a test statistic, which is a function of the sample; it is considered as a numerical summary of a set of data that...
proposed by Tukey has one degree of freedom under the null hypothesis, hence this is often called "Tukey's one-degree-of-freedom test."
Introduction
The most common setting for Tukey's test of additivity is a two-way factorial Analysis of VarianceAnalysis of variance
In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
(ANOVA) with one observation per cell. The response variable Yij is observed in a table of cells with the rows indexed by i = 1,..., m and the columns indexed by j = 1,..., n. The rows and columns typically correspond to various types and levels of treatment that are applied in combination.
The additive model states that the expected response can be expressed EYij = μ + αi + βj, where the αi and βj are unknown constant values. The unknown model parameters are usually estimated as


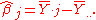
where Yi• is the mean of the ith row of the data table, Y•j is the mean of the jth column of the data table, and Y•• is the overall mean of the data table.
The additive model can be generalized to allow for arbitrary interaction effects by setting EYij = μ + αi + βj + γij. However after fitting the natural estimator of γij,
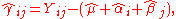
the fitted values

fit the data exactly. Thus there are no remaining degrees of freedom to estimate the variance σ2, and no hypothesis tests about the γij can performed.
Tukey therefore proposed a more constrained interaction model of the form
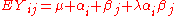
By testing the null hypothesis that λ = 0, we are able to detect some departures from additivity based only on the single parameter λ. To carry out the test, set
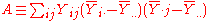

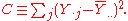
Then use the following test statistic

Under the null hypothesis, the test statistic has a F distribution with 1, q degrees of freedom, where q = mn − (m + n) is the degrees of freedom for estimating σ2.

