
Two-dimensional point vortex gas
Encyclopedia
The two-dimensional point vortex gas is a discrete particle model used to study turbulence
in two-dimensional ideal fluids. The two-dimensional guiding-center plasma is a completely equivalent model used in plasma physics.
of N points in the two-dimensional plane executing the motion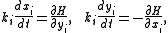
where the ki are constant and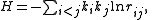
where rij is the distance between the ith and jth points.
The xi and yi are not quite canonically conjugate quantities, due to the ki in the equations of motion. The conjugate quantities are instead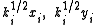
(In the confined version of the problem, the logarithmic potential is modified.)
in a two-dimensional fluid, or parallel line vortices in a three-dimensional fluid. The constant ki is the circulation of the fluid around the ith vortex. The Hamiltonian H is the interaction term of the fluid's integrated kinetic energy; it may be either positive or negative. The equations of motion simply reflect the drift of each vortex's position in the velocity field of the other vortices.
In the guiding-center plasma interpretation, the particles represent long filaments of charge parallel to some external magnetic field. The constant ki is the linear charge density
of the ith filament. The Hamiltonian H is just the two-dimensional Coulomb potential between lines. The equations of motion reflect the guiding center
drift of the charge filaments, hence the name.
Turbulence
In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
in two-dimensional ideal fluids. The two-dimensional guiding-center plasma is a completely equivalent model used in plasma physics.
General setup
The model is a Hamiltonian systemHamiltonian system
In physics and classical mechanics, a Hamiltonian system is a physical system in which forces are momentum invariant. Hamiltonian systems are studied in Hamiltonian mechanics....
of N points in the two-dimensional plane executing the motion
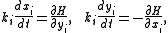
where the ki are constant and
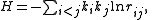
where rij is the distance between the ith and jth points.
The xi and yi are not quite canonically conjugate quantities, due to the ki in the equations of motion. The conjugate quantities are instead
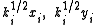
(In the confined version of the problem, the logarithmic potential is modified.)
Interpretations
In the point-vortex gas interpretation, the particles represent either point vorticesVortex
A vortex is a spinning, often turbulent,flow of fluid. Any spiral motion with closed streamlines is vortex flow. The motion of the fluid swirling rapidly around a center is called a vortex...
in a two-dimensional fluid, or parallel line vortices in a three-dimensional fluid. The constant ki is the circulation of the fluid around the ith vortex. The Hamiltonian H is the interaction term of the fluid's integrated kinetic energy; it may be either positive or negative. The equations of motion simply reflect the drift of each vortex's position in the velocity field of the other vortices.
In the guiding-center plasma interpretation, the particles represent long filaments of charge parallel to some external magnetic field. The constant ki is the linear charge density
Charge density
The linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as...
of the ith filament. The Hamiltonian H is just the two-dimensional Coulomb potential between lines. The equations of motion reflect the guiding center
Guiding center
In many cases of practical interest, the motion in a magnetic field of an electrically charged particle can be treated as the superposition of a relatively fast circular motion around a point called the guiding center and a relatively slow drift of this point...
drift of the charge filaments, hence the name.

