
Tychonoff plank
Encyclopedia
In topology
, the Tychonoff plank is a topological space
that is a counterexample
to several plausible-sounding conjecture
s. It is defined as the product
of the two ordinal space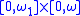
where is the first infinite ordinal
is the first infinite ordinal
and the first uncountable ordinal
the first uncountable ordinal
.
The deleted Tychonoff plank is obtained by deleting the point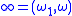 .
.
The Tychonoff plank is a compact Hausdorff space and is therefore a normal space
. However, the deleted Tychonoff plank is non-normal. Therefore the Tychonoff plank is not completely normal. This shows that a subspace of a normal space need not be normal. The Tychonoff plank is not perfectly normal because it is not a Gδ space: the singleton is closed but not a Gδ set.
is closed but not a Gδ set.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, the Tychonoff plank is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
that is a counterexample
Counterexample
In logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
to several plausible-sounding conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
s. It is defined as the product
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
of the two ordinal space
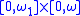
where
 is the first infinite ordinal
is the first infinite ordinalOrdinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
and
 the first uncountable ordinal
the first uncountable ordinalFirst uncountable ordinal
In mathematics, the first uncountable ordinal, traditionally denoted by ω1 or sometimes by Ω, is the smallest ordinal number that, considered as a set, is uncountable. It is the supremum of all countable ordinals...
.
The deleted Tychonoff plank is obtained by deleting the point
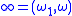 .
.The Tychonoff plank is a compact Hausdorff space and is therefore a normal space
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
. However, the deleted Tychonoff plank is non-normal. Therefore the Tychonoff plank is not completely normal. This shows that a subspace of a normal space need not be normal. The Tychonoff plank is not perfectly normal because it is not a Gδ space: the singleton
 is closed but not a Gδ set.
is closed but not a Gδ set.

