Ultraviolet catastrophe
Encyclopedia
Classical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
that an ideal black body
Black body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
at thermal equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
will emit radiation
Radiation
In physics, radiation is a process in which energetic particles or energetic waves travel through a medium or space. There are two distinct types of radiation; ionizing and non-ionizing...
with infinite power.
The term "ultraviolet catastrophe" was first used in 1911 by Paul Ehrenfest
Paul Ehrenfest
Paul Ehrenfest was an Austrian and Dutch physicist, who made major contributions to the field of statistical mechanics and its relations with quantum mechanics, including the theory of phase transition and the Ehrenfest theorem.- Biography :Paul Ehrenfest was born and grew up in Vienna in a Jewish...
, although the concept goes back to 1900 with the first derivation of the
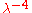dependence of the Rayleigh–Jeans law; the word "ultravioletUltraviolet
Ultraviolet light is electromagnetic radiation with a wavelength shorter than that of visible light, but longer than X-rays, in the range 10 nm to 400 nm, and energies from 3 eV to 124 eV...
" refers to the fact that the problem appears in the short wavelength region of the electromagnetic spectrum
Electromagnetic spectrum
The electromagnetic spectrum is the range of all possible frequencies of electromagnetic radiation. The "electromagnetic spectrum" of an object is the characteristic distribution of electromagnetic radiation emitted or absorbed by that particular object....
. Since the first appearance of the term, it has also been used for other predictions of a similar nature, as in quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
and such cases as ultraviolet divergence
Ultraviolet divergence
In physics, an ultraviolet divergence is a situation in which an integral, for example a Feynman diagram, diverges because of contributions of objects with very high energy , or, equivalently, because of physical phenomena at very short distances. An infinite answer to a question that should have a...
.
Problem
The ultraviolet catastrophe results from the equipartition theoremEquipartition theorem
In classical statistical mechanics, the equipartition theorem is a general formula that relates the temperature of a system with its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition...
of classical statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
which states that all harmonic oscillator
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
modes (degrees of freedom) of a system at equilibrium have an average energy of
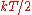.An example, from Mason's A History of the Sciences, illustrates multi-mode vibration via a piece of string. As a natural vibrator
Standing wave
In physics, a standing wave – also known as a stationary wave – is a wave that remains in a constant position.This phenomenon can occur because the medium is moving in the opposite direction to the wave, or it can arise in a stationary medium as a result of interference between two waves traveling...
, the string will oscillate with specific modes (the standing waves of a string in harmonic resonance), dependent on the length of the string. In classical physics, a radiator of energy will act as a natural vibrator. And, since each mode will have the same energy, most of the energy in a natural vibrator will be in the smaller wavelengths and higher frequencies, where most of the modes are.
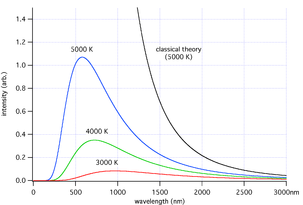
According to classical electromagnetism, the number of electromagnetic modes in a 3-dimensional cavity, per unit frequency, is proportional to the square of the frequency. This therefore implies that the radiated power per unit frequency should follow the Rayleigh–Jeans law, and be proportional to frequency squared. Thus, both the power at a given frequency and the total radiated power is unlimited as higher and higher frequencies are considered: this is clearly unphysical as the total radiated power of a cavity is not observed to be infinite, a point that was made independently by Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
and by Lord Rayleigh and Sir James Jeans in the year 1905.
Solution
Max PlanckMax Planck
Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
solved the problem by postulating that electromagnetic energy did not follow the classical description, but could only be emitted in discrete packets of energy proportional to the frequency, as given by Planck's law. This has the effect of reducing the number of possible modes with a given energy at high frequencies in the cavity described above, and thus the average energy at those frequencies by application of the equipartition theorem. The radiated power eventually goes to zero at infinite frequencies, and the total predicted power is finite. The formula for the radiated power for the idealized system (black body) was in line with known experiments, and came to be called Planck's law of black body radiation. Based on past experiments, Planck was also able to determine the value of its parameter, now called Planck's constant. The packets of energy later came to be called photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s, and played a key role in the quantum description of electromagnetism.
Historical inaccuracies
Many popular histories of physics, as well as a number of physics textbooks, present an incorrect version of the history of the ultraviolet catastrophe. In this version, the "catastrophe" was first noticed by Planck, who developed his formula in response. In fact Planck never concerned himself with this aspect of the problem, because he did not believe that the equipartition theoremEquipartition theorem
In classical statistical mechanics, the equipartition theorem is a general formula that relates the temperature of a system with its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition...
was fundamental – his motivation for introducing "quanta
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
" was entirely different. That Planck's proposal happened to provide a solution for it was realized much later, as stated above.
Though this has been known by historians for many decades, the historically incorrect version persists, in part because Planck's actual motivations for the proposal of the quantum are complicated and difficult to summarize to a modern audience.