Umklapp scattering is the transformation, like a reflection or a translation, of a wave vector to another Brillouin zone

Brillouin zone

In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...

 as a result of a scattering process, for example an electron-lattice potential scattering or an anharmonic phonon

Phonon

In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...

-phonon (or electron

Electron

The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...

-phonon) scattering

Scattering

Scattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...

 process, reflecting an electronic state

Bragg's law

In physics, Bragg's law gives the angles for coherent and incoherent scattering from a crystal lattice. When X-rays are incident on an atom, they make the electronic cloud move as does any electromagnetic wave...

 or creating a phonon with a momentum k-vector outside the first Brillouin zone

Brillouin zone

In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...

. Umklapp scattering is one process limiting the thermal conductivity in crystalline materials, the others being phonon scattering on crystal defects and at the surface of the sample.

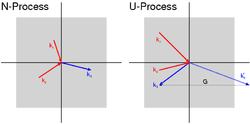
Figure 1 schematically shows the possible scattering processes of two incoming phonons with wave-vectors (k-vectors) k₁ and k₂ (red) creating one outgoing phonon with a wave vector k₃ (blue). As long as the sum of k₁ and k₂ stay inside the first Brillouin zone (gray squares) k₃ is the sum of the former two conserving phonon momentum. This process is called normal scattering (N-process).

With increasing phonon momentum and thus wave vector of k₁ and k₂ their sum might point outside the Brillouin zone (k'₃). As shown in Figure 2, k-vectors outside the first Brillouin zone are physically equivalent to vectors inside it and can be mathematically transformed into each other by the addition of a reciprocal lattice vector G. These processes are called Umklapp scattering and change the total phonon momentum.

Umklapp scattering is the dominant process for thermal resistivity at high temperatures for low defect crystals. The thermal conductivity for an insulating crystal where the U-processes are dominant has 1/T dependence.

The name derives from the German word umklappen (to turn over). Rudolf Peierls

Rudolf Peierls

Sir Rudolf Ernst Peierls, CBE was a German-born British physicist. Rudolf Peierls had a major role in Britain's nuclear program, but he also had a role in many modern sciences...

 in his autobiography "Bird of Passage" (ISBN 0-691-08390-8) states he was the originator of this phrase and coined it during his 1929 crystal lattice studies under the tutelage of Wolfgang Pauli

Wolfgang Pauli

Wolfgang Ernst Pauli was an Austrian theoretical physicist and one of the pioneers of quantum physics. In 1945, after being nominated by Albert Einstein, he received the Nobel Prize in Physics for his "decisive contribution through his discovery of a new law of Nature, the exclusion principle or...

. Peierls wrote "...I used the German term Umklapp (flip-over) and this rather ugly word has remained in use..." (page 43).