Undersampling
Encyclopedia
In signal processing
, undersampling or bandpass sampling is a technique where one samples
a bandpass filtered signal at a sample rate below the usual Nyquist rate
(twice the baseband bandwidth, i.e. twice the upper cut-off frequency), but is still able to reconstruct the signal.
When one samples a bandpass signal, the samples are equal to samples of a low-frequency alias
of the high-frequency signal. Such undersampling is also known as bandpass sampling, harmonic sampling, IF sampling, and direct IF-to-digital conversion.
In the case of the bandpass (non-baseband
) signals, with low and high band limits fL and fH respectively, the condition for an acceptable sample rate is that shifts of the bands from fL to fH and from –fH to –fL must not overlap when shifted by all integer multiples of sampling rate fs. This condition reduces to the constraint:
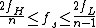, for some n satisfying: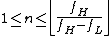 
The highest n for which the condition is satisfied leads to the lowest possible sampling rates.
Important signals of this sort include a radio's intermediate-frequency (IF) or radio-frequency (RF) signal.
If n > 1, then the conditions result in what is sometimes referred to as undersampling, bandpass sampling, or using a sampling rate less than the Nyquist rate 2fH obtained from the upper bound of the spectrum. See aliasing
for a simpler formulation of this Nyquist criterion that specifies the lower bound on sampling rate (but is incomplete because it does not specify the gaps above that bound, in which aliasing will occur). Alternatively, for the case of a given sampling frequency, simpler formulae for the constraints on the signal's spectral band are given below.
As we have seen, the normal baseband
condition for reversible sampling is that X(f) = 0 outside the open interval:
,
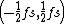and the reconstructive interpolation function, or lowpass filter impulse response, is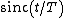
.
To accommodate undersampling, the bandpass condition is that X(f) = 0 outside the union of open positive and negative frequency bands
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, undersampling or bandpass sampling is a technique where one samples
Sampling (signal processing)
In signal processing, sampling is the reduction of a continuous signal to a discrete signal. A common example is the conversion of a sound wave to a sequence of samples ....
a bandpass filtered signal at a sample rate below the usual Nyquist rate
Nyquist rate
In signal processing, the Nyquist rate, named after Harry Nyquist, is two times the bandwidth of a bandlimited signal or a bandlimited channel...
(twice the baseband bandwidth, i.e. twice the upper cut-off frequency), but is still able to reconstruct the signal.
When one samples a bandpass signal, the samples are equal to samples of a low-frequency alias
Aliasing
In signal processing and related disciplines, aliasing refers to an effect that causes different signals to become indistinguishable when sampled...
of the high-frequency signal. Such undersampling is also known as bandpass sampling, harmonic sampling, IF sampling, and direct IF-to-digital conversion.
Description
Real-valued signals have Fourier spectra with symmetry about zero. That is, they have a negative-frequency spectrum that is a mirror image of the positive-frequency spectrum. Sampling effectively shifts both sides of the spectrum by multiples of the sampling frequency. The criterion to avoid aliasing is that none of these shifted copies of the spectrum overlap.In the case of the bandpass (non-baseband
Baseband
In telecommunications and signal processing, baseband is an adjective that describes signals and systems whose range of frequencies is measured from close to 0 hertz to a cut-off frequency, a maximum bandwidth or highest signal frequency; it is sometimes used as a noun for a band of frequencies...
) signals, with low and high band limits fL and fH respectively, the condition for an acceptable sample rate is that shifts of the bands from fL to fH and from –fH to –fL must not overlap when shifted by all integer multiples of sampling rate fs. This condition reduces to the constraint:
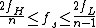, for some n satisfying: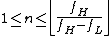 The highest n for which the condition is satisfied leads to the lowest possible sampling rates.
Important signals of this sort include a radio's intermediate-frequency (IF) or radio-frequency (RF) signal.
If n > 1, then the conditions result in what is sometimes referred to as undersampling, bandpass sampling, or using a sampling rate less than the Nyquist rate 2fH obtained from the upper bound of the spectrum. See aliasing
Aliasing
In signal processing and related disciplines, aliasing refers to an effect that causes different signals to become indistinguishable when sampled...
for a simpler formulation of this Nyquist criterion that specifies the lower bound on sampling rate (but is incomplete because it does not specify the gaps above that bound, in which aliasing will occur). Alternatively, for the case of a given sampling frequency, simpler formulae for the constraints on the signal's spectral band are given below.
- Example: Consider FM radio to illustrate the idea of undersampling.
- In the US, FM radio operates on the frequency band from fL = 88 MHz to fH = 108 MHz. The bandwidth is given by
- The sampling conditions are satisfied for
- Therefore, n can be 1, 2, 3, 4, or 5.
- The value n = 5 gives the lowest sampling frequencies interval
and this is a scenario of undersampling. In this case, the signal spectrum fits between 2 and 2.5 times the sampling rate (higher than 86.4–88 MHz but lower than 108–110 MHz).
- A lower value of n will also lead to a useful sampling rate. For example, using n = 4, the FM band spectrum fits easily between 1.5 and 2.0 times the sampling rate, for a sampling rate near 56 MHz (multiples of the Nyquist frequency being 28, 56, 84, 112, etc.). See the illustrations at the right.
- When undersampling a real-world signal, the sampling circuit must be fast enough to capture the highest signal frequency of interest. Theoretically, each sample should be taken during an infinitesimally short interval, but this is not practically feasible. Instead, the sampling of the signal should be made in a short enough interval that it can represent the instantaneous value of the signal with the highest frequency. This means that in the FM radio example above, the sampling circuit must be able to capture a signal with a frequency of 108 MHz, not 43.2 MHz. Thus, the sampling frequency may be only a little bit greater than 43.2 MHz, but the input bandwidth of the system must be at least 108 MHz. Similarly, the accuracy of the sampling timing, or aperture uncertainty of the sampler, frequently the analog-to-digital converterAnalog-to-digital converterAn analog-to-digital converter is a device that converts a continuous quantity to a discrete time digital representation. An ADC may also provide an isolated measurement...
, must be appropriate for the frequencies being sampled 108MHz, not the lower sample rate.
- If the sampling theorem is interpreted as requiring twice the highest frequency, then the required sampling rate would be assumed to be greater than the Nyquist rate 216 MHz. While this does satisfy the last condition on the sampling rate, it is grossly oversampled.
- Note that if a band is sampled with n > 1, then a band-pass filterBand-pass filterA band-pass filter is a device that passes frequencies within a certain range and rejects frequencies outside that range.Optical band-pass filters are of common usage....
is required for the anti-aliasing filterAnti-aliasing filterAn anti-aliasing filter is a filter used before a signal sampler, to restrict the bandwidth of a signal to approximately satisfy the sampling theorem....
, instead of a lowpass filter.
As we have seen, the normal baseband
Baseband
In telecommunications and signal processing, baseband is an adjective that describes signals and systems whose range of frequencies is measured from close to 0 hertz to a cut-off frequency, a maximum bandwidth or highest signal frequency; it is sometimes used as a noun for a band of frequencies...
condition for reversible sampling is that X(f) = 0 outside the open interval:
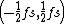,and the reconstructive interpolation function, or lowpass filter impulse response, is
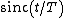.To accommodate undersampling, the bandpass condition is that X(f) = 0 outside the union of open positive and negative frequency bands
-
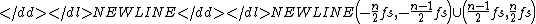for some positive integer 
.
-
- which includes the normal basebandBasebandIn telecommunications and signal processing, baseband is an adjective that describes signals and systems whose range of frequencies is measured from close to 0 hertz to a cut-off frequency, a maximum bandwidth or highest signal frequency; it is sometimes used as a noun for a band of frequencies...
condition as case n = 1 (except that where the intervals come together at 0 frequency, they can be closed).
- which includes the normal baseband
The corresponding interpolation function is the bandpass filter given by this difference of lowpass impulse responses:
-
.
On the other hand, reconstruction is not usually the goal with sampled IF or RF signals. Rather, the sample sequence can be treated as ordinary samples of the signal frequency-shifted to near baseband, and digital demodulation can proceed on that basis, recognizing the spectrum mirroring when n is even.
Further generalizations of undersampling for the case of signals with multiple bands are possible, and signals over multidimensional domains (space or space-time) and have been worked out in detail by Igor KluvánekIgor KluvánekIgor Kluvánek was a Slovak-Australian mathematician.-Academic career:Igor Kluvánek obtained his first degree in electrical engineering from the Slovak Polytechnic University, Bratislava, in 1953. His first appointment was in the Department of Mathematics of the same institution. At the same time...
.-