
Uniformly convex space
Encyclopedia
In mathematics
, uniformly convex spaces are common examples of reflexive
Banach space
s. The concept of uniform convexity was first introduced by James A. Clarkson in 1936.
so that, for every there is some
there is some 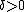 so that for any two vectors with
so that for any two vectors with 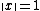 and
and 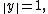
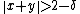
implies
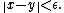
Intuitively, the center of a line segment inside the unit ball must lie deep inside the unit ball unless the segment is short.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, uniformly convex spaces are common examples of reflexive
Reflexive space
In functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C...
Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. The concept of uniform convexity was first introduced by James A. Clarkson in 1936.
Definition
A uniformly convex space is a normed vector spaceNormed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
so that, for every
 there is some
there is some 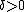 so that for any two vectors with
so that for any two vectors with 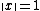 and
and 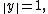
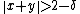
implies
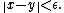
Intuitively, the center of a line segment inside the unit ball must lie deep inside the unit ball unless the segment is short.
Properties
- The Milman–Pettis theoremMilman–Pettis theoremIn mathematics, the Milman–Pettis theorem states that every uniformly convex Banach space is reflexive.The theorem was proved independently by D. Milman and B. J. Pettis . S. Kakutani gave a different proof in , and John R. Ringrose published a shorter proof in 1959.- References :* S. Kakutani,...
states that every uniformly convex Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
is reflexiveReflexive spaceIn functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C...
, while the converse is not true. - If
 is a sequence in a uniformly convex Banach space which converges weakly to
is a sequence in a uniformly convex Banach space which converges weakly to 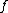 and satisfies
and satisfies 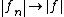 , then
, then 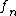 converges strongly to
converges strongly to 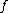 , that is,
, that is, 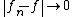 .
. - A Banach space
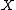 is uniformly convex if and only if its dual
is uniformly convex if and only if its dual 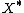 is uniformly smooth.
is uniformly smooth.
Examples
- Every Hilbert space is uniformly convex.
- Hanner's inequalitiesHanner's inequalitiesIn mathematics, Hanner's inequalities are results in the theory of Lp spaces. Their proof was published in 1956 by Olof Hanner. They provide a simpler way of proving the uniform convexity of Lp spaces for p ∈ than the approach proposed by James Clarkson in 1936.-Statement of the...
imply that Lp spacesLp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
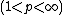 are uniformly convex.
are uniformly convex.

