Urysohn's lemma
Encyclopedia
In topology
, Urysohn's lemma is a lemma
that states that a topological space
is normal
if and only if any two disjoint closed subsets
can be separated by a function.
Urysohn's lemma is sometimes called "the first non-trivial fact of point set topology" and is commonly used to construct continuous functions with various properties on normal spaces. It is widely applicable since all metric space
s and all compact
Hausdorff space
s are normal. The lemma is generalized by (and usually used in the proof of) the Tietze extension theorem.
The lemma is named after the mathematician
Pavel Samuilovich Urysohn
.
A and B of a topological space
X are said to be separated by neighbourhoods if there are neighbourhoods U of A and V of B that are also disjoint. A and B are said to be separated by a function if there exists a continuous function f from X into the unit interval
[0,1] such that f(a) = 0 for all a in A and f(b) = 1 for all b in B. Any such function is called a Urysohn function for A and B.
A normal space
is a topological space in which any two disjoint closed sets can be separated by neighbourhoods. Urysohn's lemma states that a topological space is normal if and only if any two disjoint closed sets can be separated by a function.
The sets A and B need not be precisely separated by f, i.e., we do not, and in general cannot, require that f(x) ≠ 0 and ≠ 1 for x outside of A and B. This is possible only in perfectly normal spaces.
Urysohn's lemma has led to the formulation of other topological properties such as the 'Tychonoff property' and 'completely Hausdorff spaces'. For example, a corollary of the lemma is that normal T1 spaces
are Tychonoff
.
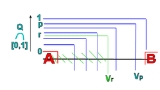
 For every dyadic fraction r ∈ (0,1), we are going to construct an open subset
For every dyadic fraction r ∈ (0,1), we are going to construct an open subset
U(r) of X such that:
Once we have these sets, we define f(x) = inf
{ r : x ∈ U(r) } for every x ∈ X. Using the fact that the dyadic rationals are dense, it is then not too hard to show that f is continuous and has the property f(A) ⊆ {0} and f(B) ⊆ {1}.
In order to construct the sets U(r), we actually do a little bit more: we construct sets U(r) and V(r) such that
Since the complement of V(r) is closed and contains U(r), the latter condition then implies condition (2) from above.
This construction proceeds by mathematical induction
. Since X is normal, we can find two disjoint open sets U(1/2) and V(1/2) which contain A and B, respectively. Now assume that n≥1 and the sets U(a/2n) and V(a/2n) have already been constructed for a = 1,...,2n-1. Since X is normal, we can find two disjoint open sets which contain the complement of V(a/2n) and the complement of U((a+1)/2n), respectively. Call these two open sets U((2a+1)/2n+1) and V((2a+1)/2n+1), and verify the above three conditions.
The Mizar project
has completely formalized and automatically checked a proof of Urysohn's lemma in the URYSOHN3 file.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, Urysohn's lemma is a lemma
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
that states that a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is normal
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
if and only if any two disjoint closed subsets
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
can be separated by a function.
Urysohn's lemma is sometimes called "the first non-trivial fact of point set topology" and is commonly used to construct continuous functions with various properties on normal spaces. It is widely applicable since all metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s and all compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s are normal. The lemma is generalized by (and usually used in the proof of) the Tietze extension theorem.
The lemma is named after the mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Pavel Samuilovich Urysohn
Pavel Samuilovich Urysohn
Pavel Samuilovich Urysohn, Pavel Uryson was a Jewish mathematician who is best known for his contributions in the theory of dimension, and for developing Urysohn's Metrization Theorem and Urysohn's Lemma, both of which are fundamental results in topology...
.
Formal statement
Two disjoint closed subsetsClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
A and B of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X are said to be separated by neighbourhoods if there are neighbourhoods U of A and V of B that are also disjoint. A and B are said to be separated by a function if there exists a continuous function f from X into the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
A normal space
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
is a topological space in which any two disjoint closed sets can be separated by neighbourhoods. Urysohn's lemma states that a topological space is normal if and only if any two disjoint closed sets can be separated by a function.
The sets A and B need not be precisely separated by f, i.e., we do not, and in general cannot, require that f(x) ≠ 0 and ≠ 1 for x outside of A and B. This is possible only in perfectly normal spaces.
Urysohn's lemma has led to the formulation of other topological properties such as the 'Tychonoff property' and 'completely Hausdorff spaces'. For example, a corollary of the lemma is that normal T1 spaces
T1 space
In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
are Tychonoff
Tychonoff space
In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
.
Sketch of proof

Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
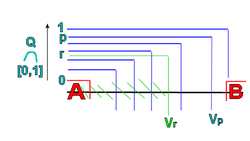
U(r) of X such that:
- U(r) contains A and is disjoint from B for all r
- for r < s, the closureClosure (topology)In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of U(r) is contained in U(s).
Once we have these sets, we define f(x) = inf
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
{ r : x ∈ U(r) } for every x ∈ X. Using the fact that the dyadic rationals are dense, it is then not too hard to show that f is continuous and has the property f(A) ⊆ {0} and f(B) ⊆ {1}.
In order to construct the sets U(r), we actually do a little bit more: we construct sets U(r) and V(r) such that
- A ⊆ U(r) and B ⊆ V(r) for all r
- U(r) and V(r) are open and disjoint for all r
- for r < s, V(s) is contained in the complement of U(r) and the complement of V(r) is contained in U(s).
Since the complement of V(r) is closed and contains U(r), the latter condition then implies condition (2) from above.
This construction proceeds by mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. Since X is normal, we can find two disjoint open sets U(1/2) and V(1/2) which contain A and B, respectively. Now assume that n≥1 and the sets U(a/2n) and V(a/2n) have already been constructed for a = 1,...,2n-1. Since X is normal, we can find two disjoint open sets which contain the complement of V(a/2n) and the complement of U((a+1)/2n), respectively. Call these two open sets U((2a+1)/2n+1) and V((2a+1)/2n+1), and verify the above three conditions.
The Mizar project
Mizar system
The Mizar system consists of a language for writing strictly formalized mathematical definitions and proofs, a computer program which is able to check proofs written in this language, and a library of definitions and proved theorems which can be referenced and used in new articles. Mizar has goals...
has completely formalized and automatically checked a proof of Urysohn's lemma in the URYSOHN3 file.

