VC dimension
Encyclopedia
In statistical learning theory
, or sometimes computational learning theory
, the VC dimension (for Vapnik–Chervonenkis dimension) is a measure of the capacity
of a statistical classification algorithm
, defined as the cardinality of the largest set of points that the algorithm can shatter. It is a core concept in Vapnik–Chervonenkis theory, and was originally defined by Vladimir Vapnik
and Alexey Chervonenkis
.
Informally, the capacity of a classification model is related to how complicated it can be. For example, consider the thresholding
of a high-degree
polynomial
: if the polynomial evaluates above zero, that point is classified as positive, otherwise as negative. A high-degree polynomial can be wiggly, so it can fit a given set of training points well. But one can expect that the classifier will make errors on other points, because it is too wiggly. Such a polynomial has a high capacity. A much simpler alternative is to threshold a linear function. This polynomial may not fit the training set well, because it has a low capacity. We make this notion of capacity more rigorous below.
with some parameter vector 
is said to shatter a set of data points 
if, for all assignments of labels to those points, there exists a 
such that the model 
makes no errors when evaluating that set of data points.
VC dimension of a model
is 
where 
is the maximum 
such that some data point set of cardinality 
can be shattered by 
.
For example, consider a straight line
as the classification model: the model used by a perceptron
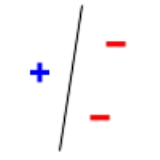
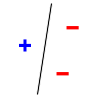
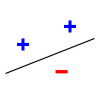
. The line should separate positive data points from negative data points. There exist sets of 3 points that can indeed be shattered using this model (any 3 points that are not collinear can be shattered). However, no set of 4 points can be shattered: by Radon's theorem
, any four points can be partitioned into two subsets with intersecting convex hulls, so it is not possible to separate one of these two subsets from the other. Thus, the VC dimension of this particular classifier is 3. It is important to remember that one can choose the arrangement of points, but then cannot change it as the labels on the points are considered. Note, only 3 of the 23 = 8 possible label assignments are shown for the three points.
on the test error of a classification model.
The bound on the test error of a classification model (on data that is drawn i.i.d. from the same distribution as the training set) is given by
with probability
, where 
is the VC dimension of the classification model, and 
is the size of the training set (restriction: this formula is valid when 
). Similar complexity bounds can be derived using Rademacher complexity
, but Rademacher complexity can sometimes provide more insight than VC dimension calculations into such statistical methods such as those using kernels
.
In computational geometry
, VC dimension is one of the critical parameters in the size of ε-nets, which determines the complexity of approximation algorithms based on them; range sets without finite VC dimension may not have finite ε-nets at all.
Statistical learning theory
Statistical learning theory is an ambiguous term.#It may refer to computational learning theory, which is a sub-field of theoretical computer science that studies how algorithms can learn from data....
, or sometimes computational learning theory
Computational learning theory
In theoretical computer science, computational learning theory is a mathematical field related to the analysis of machine learning algorithms.-Overview:Theoretical results in machine learning mainly deal with a type of...
, the VC dimension (for Vapnik–Chervonenkis dimension) is a measure of the capacity
Membership function (mathematics)
The membership function of a fuzzy set is a generalization of the indicator function in classical sets. In fuzzy logic, it represents the degree of truth as an extension of valuation. Degrees of truth are often confused with probabilities, although they are conceptually distinct, because fuzzy...
of a statistical classification algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
, defined as the cardinality of the largest set of points that the algorithm can shatter. It is a core concept in Vapnik–Chervonenkis theory, and was originally defined by Vladimir Vapnik
Vladimir Vapnik
Vladimir Naumovich Vapnik is one of the main developers of Vapnik–Chervonenkis theory. He was born in the Soviet Union. He received his master's degree in mathematics at the Uzbek State University, Samarkand, Uzbek SSR in 1958 and Ph.D in statistics at the Institute of Control Sciences, Moscow in...
and Alexey Chervonenkis
Alexey Chervonenkis
Alexey Jakovlevich Chervonenkis is a Soviet and Russian mathematician, and, with Vladimir Vapnik, was one of the main developers of the Vapnik–Chervonenkis theory, also known as the "fundamental theory of learning" an important part of computational learning theory. As of September 2007, Dr...
.
Informally, the capacity of a classification model is related to how complicated it can be. For example, consider the thresholding
Heaviside step function
The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
of a high-degree
Degree (mathematics)
In mathematics, there are several meanings of degree depending on the subject.- Unit of angle :A degree , usually denoted by ° , is a measurement of a plane angle, representing 1⁄360 of a turn...
polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
: if the polynomial evaluates above zero, that point is classified as positive, otherwise as negative. A high-degree polynomial can be wiggly, so it can fit a given set of training points well. But one can expect that the classifier will make errors on other points, because it is too wiggly. Such a polynomial has a high capacity. A much simpler alternative is to threshold a linear function. This polynomial may not fit the training set well, because it has a low capacity. We make this notion of capacity more rigorous below.
Shattering
A classification model with some parameter vector is said to shatter a set of data points if, for all assignments of labels to those points, there exists a such that the model makes no errors when evaluating that set of data points.VC dimension of a model
is where is the maximum such that some data point set of cardinality can be shattered by .For example, consider a straight line
Linear classifier
In the field of machine learning, the goal of statistical classification is to use an object's characteristics to identify which class it belongs to. A linear classifier achieves this by making a classification decision based on the value of a linear combination of the characteristics...
as the classification model: the model used by a perceptron
Perceptron
The perceptron is a type of artificial neural network invented in 1957 at the Cornell Aeronautical Laboratory by Frank Rosenblatt. It can be seen as the simplest kind of feedforward neural network: a linear classifier.- Definition :...
. The line should separate positive data points from negative data points. There exist sets of 3 points that can indeed be shattered using this model (any 3 points that are not collinear can be shattered). However, no set of 4 points can be shattered: by Radon's theorem
Radon's theorem
In geometry, Radon's theorem on convex sets, named after Johann Radon, states that any set of d + 2 points in Rd can be partitioned into two sets whose convex hulls intersect...
, any four points can be partitioned into two subsets with intersecting convex hulls, so it is not possible to separate one of these two subsets from the other. Thus, the VC dimension of this particular classifier is 3. It is important to remember that one can choose the arrangement of points, but then cannot change it as the labels on the points are considered. Note, only 3 of the 23 = 8 possible label assignments are shown for the three points.
 |
 |
 |
|
| 3 points shattered | 4 points impossible | ||
Uses
The VC dimension has utility in statistical learning theory, because it can predict a probabilistic upper boundUpper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
on the test error of a classification model.
The bound on the test error of a classification model (on data that is drawn i.i.d. from the same distribution as the training set) is given by
with probability
, where is the VC dimension of the classification model, and is the size of the training set (restriction: this formula is valid when ). Similar complexity bounds can be derived using Rademacher complexityRademacher complexity
In statistics and machine learning, Rademacher complexity, named after Hans Rademacher, measures richness of a class of real-valued functions with respect to a probability distribution....
, but Rademacher complexity can sometimes provide more insight than VC dimension calculations into such statistical methods such as those using kernels
Kernel methods
In computer science, kernel methods are a class of algorithms for pattern analysis, whose best known elementis the support vector machine...
.
In computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
, VC dimension is one of the critical parameters in the size of ε-nets, which determines the complexity of approximation algorithms based on them; range sets without finite VC dimension may not have finite ε-nets at all.