Vandiver's conjecture
Encyclopedia
In mathematics
, the Kummer–Vandiver conjecture, or Vandiver conjecture, states that a prime p does not divide the class number hK of the maximal real subfield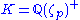
of the p-th cyclotomic field
.
The conjecture was first made by Ernst Kummer
in 1849 December 28 and 1853 April 24 in letters to Leopold Kronecker
, reprinted in , and independently rediscovered around 1920 by Philipp Furtwängler
and ,
As of 2011, there is no particularly strong evidence either for or against the conjecture and it is unclear whether it is true or false, though it is likely that counterexamples are very rare.
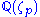is a product of two integers h1 and h2, called the first and second factors of the class number, where h2 is the class number of the maximal real subfield 
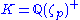of the p-th cyclotomic field
. The first factor h1 is well understood and can be written explicitly in terms of Bernoulli numbers, and is usually rather large. The second factor h2 is not well understood and seems hard to compute explicitly.
Kummer showed that if a prime p does not divide the class number h, then Fermat's last theorem holds for exponent p.
Kummer also showed that if p divides the second factor, then it also divides the first factor. In particular the Kummer–Vandiver conjecture holds for regular primes.
verified it for p < 12 million. extended this to primes less than 237, about 1011.
describes an informal probability argument, based on rather dubious assumptions about the equidistribution of class numbers mod p, suggesting that the number of primes less than x that are exceptions to Vandiver's conjecture might grow like (1/2)log log x. This grows extremely slowly, and suggests that the computer calculations do not provide much evidence for Vandiver's conjecture: for example, the probability argument (combined with the calculations for small primes) suggests that one should only expect about 1 counterexample in the first 10100 primes, suggesting that it is unlikely any counterexample will be found by further brute force searches even if there are an infinite number of exceptions.
gave a refined version of Washington's heuristic argument, suggesting that Vandiver's conjecture is probably true.
gave conjectural calculations of the class numbers of real cyclotomic fields for primes up to 10000, which strongly suggest that the class numbers are not randomly distributed mod p. They tend to be quite small and are often just 1. For example, assuming the generalized Riemann hypothesis
, the class number of the real cyclotomic field for the prime p is 1 for p<163, and divisible by 4 for p=163.
of the integers, namely that
whenever n is a multiple of 4. In fact from Vandiver's conjecture and the norm residue isomorphism theorem
follows a full conjectural calculation of the K-groups for all values of n; see Quillen–Lichtenbaum conjecture
for details.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Kummer–Vandiver conjecture, or Vandiver conjecture, states that a prime p does not divide the class number hK of the maximal real subfield
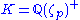of the p-th cyclotomic fieldCyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
.
The conjecture was first made by Ernst Kummer
Ernst Kummer
Ernst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
in 1849 December 28 and 1853 April 24 in letters to Leopold Kronecker
Leopold Kronecker
Leopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...
, reprinted in , and independently rediscovered around 1920 by Philipp Furtwängler
Philipp Furtwängler
Philipp Furtwängler was a German number theorist.He wrote an 1896 doctoral dissertation at the University of Göttingen on cubic forms , under Felix Klein...
and ,
As of 2011, there is no particularly strong evidence either for or against the conjecture and it is unclear whether it is true or false, though it is likely that counterexamples are very rare.
Background
The class number h of the cyclotomic field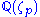 is a product of two integers h1 and h2, called the first and second factors of the class number, where h2 is the class number of the maximal real subfield 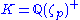of the p-th cyclotomic fieldCyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
. The first factor h1 is well understood and can be written explicitly in terms of Bernoulli numbers, and is usually rather large. The second factor h2 is not well understood and seems hard to compute explicitly.
Kummer showed that if a prime p does not divide the class number h, then Fermat's last theorem holds for exponent p.
Kummer also showed that if p divides the second factor, then it also divides the first factor. In particular the Kummer–Vandiver conjecture holds for regular primes.
Evidence for and against Vandiver's conjecture
Kummer verified Vandiver's conjecture for p less than 200, and Vandiver extended this to p less than 600.verified it for p < 12 million. extended this to primes less than 237, about 1011.
describes an informal probability argument, based on rather dubious assumptions about the equidistribution of class numbers mod p, suggesting that the number of primes less than x that are exceptions to Vandiver's conjecture might grow like (1/2)log log x. This grows extremely slowly, and suggests that the computer calculations do not provide much evidence for Vandiver's conjecture: for example, the probability argument (combined with the calculations for small primes) suggests that one should only expect about 1 counterexample in the first 10100 primes, suggesting that it is unlikely any counterexample will be found by further brute force searches even if there are an infinite number of exceptions.
gave a refined version of Washington's heuristic argument, suggesting that Vandiver's conjecture is probably true.
gave conjectural calculations of the class numbers of real cyclotomic fields for primes up to 10000, which strongly suggest that the class numbers are not randomly distributed mod p. They tend to be quite small and are often just 1. For example, assuming the generalized Riemann hypothesis
Generalized Riemann hypothesis
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...
, the class number of the real cyclotomic field for the prime p is 1 for p<163, and divisible by 4 for p=163.
Consequences of Vandiver's conjecture
showed that the conjecture is equivalent to a statement in the algebraic K-theoryAlgebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
of the integers, namely that
- Kn(Z) = 0
whenever n is a multiple of 4. In fact from Vandiver's conjecture and the norm residue isomorphism theorem
Norm residue isomorphism theorem
In the mathematical field of algebraic K-theory, the norm residue isomorphism theorem is a long-sought result whose complete proof was announced in 2009...
follows a full conjectural calculation of the K-groups for all values of n; see Quillen–Lichtenbaum conjecture
Quillen–Lichtenbaum conjecture
In mathematics, the Quillen–Lichtenbaum conjecture is a conjecture relating étale cohomology to algebraic K-theory introduced by , who was inspired by earlier conjectures of . and proved the Quillen–Lichtenbaum conjecture at the prime 2 for some number fields...
for details.