
Norm residue isomorphism theorem
Encyclopedia
In the mathematical field of algebraic K-theory
, the norm residue isomorphism theorem is a long-sought result whose complete proof was announced in 2009. It previously was known as the Bloch–Kato conjecture, after Spencer Bloch
and Kazuya Kato
, or more precisely the motivic Bloch–Kato conjecture in some places, since there is another Bloch–Kato conjecture on values of L-functions.
It is a generalisation of the Milnor conjecture
of K-theory, which was proved in the 1990s by Vladimir Voevodsky
, the Milnor conjecture being the 2-torsion part of the Bloch–Kato conjecture. The point of the conjecture is to equate the torsion in a K-group of a field
F, algebraic information that is in general relatively inaccessible, with the torsion in a Galois cohomology
group for F, which is in many cases much easier to compute. Now that the complete proof of the Bloch–Kato conjecture has been announced, due to several mathematicians and contained in quite a number of papers, the result is also known as the Voevodsky–Rost theorem, for Voevodsky and Markus Rost
. The title "norm residue" uses the analogy with standard local class field theory to identify the result conjectured and now announced in terms of its function in a "higher" class field theory, still being developed.
The norm residue isomorphism theorem implies the Quillen–Lichtenbaum conjecture
.
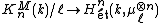
from Milnor K-theory
mod l to étale cohomology
is an isomorphism. The corresponding statement for l=2 is the Milnor conjecture
that was proved earlier by Voevodsky.
Algebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
, the norm residue isomorphism theorem is a long-sought result whose complete proof was announced in 2009. It previously was known as the Bloch–Kato conjecture, after Spencer Bloch
Spencer Bloch
Spencer Janney Bloch is an American mathematician known for his contributions to algebraic geometry and algebraic K-theory. Bloch is a R. M. Hutchins Distinguished Service Professor Emeritus in the Department of Mathematics of the University of Chicago. He is a member of the U.S...
and Kazuya Kato
Kazuya Kato
is a Japanese mathematician. He grew up in the prefecture of Wakayama in Japan. He attended college at the University of Tokyo, from which he also obtained his master's degree in 1975, and his PhD in 1980. He was a professor at Tokyo University, Tokyo Institute of Technology and Kyoto University...
, or more precisely the motivic Bloch–Kato conjecture in some places, since there is another Bloch–Kato conjecture on values of L-functions.
It is a generalisation of the Milnor conjecture
Milnor conjecture
In mathematics, the Milnor conjecture was a proposal by of a description of the Milnor K-theory of a general field F with characteristic different from 2, by means of the Galois cohomology of F with coefficients in Z/2Z. It was proved by .-Statement of the theorem:Let F be a field of...
of K-theory, which was proved in the 1990s by Vladimir Voevodsky
Vladimir Voevodsky
Vladimir Voevodsky is a Russian American mathematician. His work in developing a homotopy theory for algebraic varieties and formulating motivic cohomology led to the award of a Fields Medal in 2002.- Biography :...
, the Milnor conjecture being the 2-torsion part of the Bloch–Kato conjecture. The point of the conjecture is to equate the torsion in a K-group of a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F, algebraic information that is in general relatively inaccessible, with the torsion in a Galois cohomology
Galois cohomology
In mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
group for F, which is in many cases much easier to compute. Now that the complete proof of the Bloch–Kato conjecture has been announced, due to several mathematicians and contained in quite a number of papers, the result is also known as the Voevodsky–Rost theorem, for Voevodsky and Markus Rost
Markus Rost
Markus Rost is a German mathematician who works at the intersection of topology and algebra. He was an invited speaker at the International Congress of Mathematicians in 2002 in Beijing, China...
. The title "norm residue" uses the analogy with standard local class field theory to identify the result conjectured and now announced in terms of its function in a "higher" class field theory, still being developed.
The norm residue isomorphism theorem implies the Quillen–Lichtenbaum conjecture
Quillen–Lichtenbaum conjecture
In mathematics, the Quillen–Lichtenbaum conjecture is a conjecture relating étale cohomology to algebraic K-theory introduced by , who was inspired by earlier conjectures of . and proved the Quillen–Lichtenbaum conjecture at the prime 2 for some number fields...
.
Statement
The norm residue isomorphism theorem (or Bloch-Kato conjecture) states that for a field k and an odd prime l that is invertible in k, the norm residue map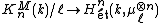
from Milnor K-theory
Milnor K-theory
In mathematics, Milnor K-theory was an early attempt to define higher algebraic K-theory, introduced by .The calculation of K2 of a field k led Milnor to the following ad hoc definition of "higher" K-groups by...
mod l to étale cohomology
Étale cohomology
In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
is an isomorphism. The corresponding statement for l=2 is the Milnor conjecture
Milnor conjecture
In mathematics, the Milnor conjecture was a proposal by of a description of the Milnor K-theory of a general field F with characteristic different from 2, by means of the Galois cohomology of F with coefficients in Z/2Z. It was proved by .-Statement of the theorem:Let F be a field of...
that was proved earlier by Voevodsky.

