Milnor K-theory
Encyclopedia
In mathematics, Milnor K-theory was an early attempt to define higher algebraic K-theory
, introduced by .
The calculation of K2 of a field k led Milnor to the following ad hoc definition of "higher" K-groups by
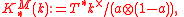
thus as graded parts of a quotient of the tensor algebra
of the multiplicative group
k× by the two-sided ideal, generated by the
for a ≠ 0, 1. For n = 0,1,2 these coincide with Quillen's K-groups of a field, but for n ≧ 3 they differ in general. For example, we have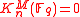
for n ≧ 3.
Milnor K-theory modulo 2 is related to étale
(or Galois
) cohomology of the field by the Milnor conjecture
, proven by Voevodsky. The analogous statement for odd primes is the Bloch–Kato conjecture, proved by Voevodsky, Rost, and others.
Algebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
, introduced by .
The calculation of K2 of a field k led Milnor to the following ad hoc definition of "higher" K-groups by
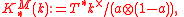
thus as graded parts of a quotient of the tensor algebra
Tensor algebra
In mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
of the multiplicative group
Multiplicative group
In mathematics and group theory the term multiplicative group refers to one of the following concepts, depending on the context*any group \scriptstyle\mathfrak \,\! whose binary operation is written in multiplicative notation ,*the underlying group under multiplication of the invertible elements of...
k× by the two-sided ideal, generated by the
for a ≠ 0, 1. For n = 0,1,2 these coincide with Quillen's K-groups of a field, but for n ≧ 3 they differ in general. For example, we have
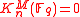for n ≧ 3.Milnor K-theory modulo 2 is related to étale
Étale cohomology
In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
(or Galois
Galois cohomology
In mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
) cohomology of the field by the Milnor conjecture
Milnor conjecture
In mathematics, the Milnor conjecture was a proposal by of a description of the Milnor K-theory of a general field F with characteristic different from 2, by means of the Galois cohomology of F with coefficients in Z/2Z. It was proved by .-Statement of the theorem:Let F be a field of...
, proven by Voevodsky. The analogous statement for odd primes is the Bloch–Kato conjecture, proved by Voevodsky, Rost, and others.