
Velocity-addition formula
Encyclopedia
In physics
, a velocity-addition formula is an equation that relates the velocities of moving objects in different reference frame
s.
observed, if a ship is moving relative to the shore at velocity , and a fly is moving with velocity
, and a fly is moving with velocity 
as measured on the ship, calculating the velocity of the fly as measured on the shore is what is meant by the addition of the velocities
 and
and  . When both the fly and the ship are moving slowly compared to light, it is accurate enough to use the vector sum
. When both the fly and the ship are moving slowly compared to light, it is accurate enough to use the vector sum
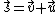
where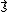 is the velocity of the fly relative to the shore.
is the velocity of the fly relative to the shore.
, the frame of the ship has a different clock rate and distance measure, and the notion of simultaneity in the direction of motion is altered, so the addition law for velocities is changed. This change isn't noticeable at low velocities but as the velocity increases towards the speed of light it becomes important. The addition law is also called a composition law for velocities. For collinear motions, the velocity of the fly relative to the shore is given by
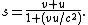
This is also the law of addition of hyperbolic tangents
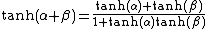
where
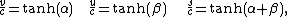
which shows that the composition of collinear velocities is associative and commutative. The quantities and
and  are called rapidities
are called rapidities
. The reason that the velocities are hyperbolic tangents is because the Lorentz transformation
can be thought of as the application of a hyperbolic rotation through a hyperbolic angle
which is the rapidity
. Suppose the velocity of a line in space-time is the slope
of the line, which is the hyperbolic tangent of the rapidity, just as the slope of the -axis after a rotation is given by the tangent of the rotation angle. When a plane is successively rotated by two angles, the final rotation is by the sum of the two angles. So the final slope of the
-axis after a rotation is given by the tangent of the rotation angle. When a plane is successively rotated by two angles, the final rotation is by the sum of the two angles. So the final slope of the  -axis is the tangent of the sum of the two angles. In the same way, the slope of the time axis after two boosts is the hyperbolic tangent of the sum of the two rapidities.
-axis is the tangent of the sum of the two angles. In the same way, the slope of the time axis after two boosts is the hyperbolic tangent of the sum of the two rapidities.
The colinear law of composition of velocities gave the first test of the kinematics of the special theory of relativity. Using a Michelson interferometer
, Fizeau
measured
the speed of light in a fluid moving parallel to the light. The speed of
light in the fluid is slower than the speed of light in vacuum, and it changes if the fluid is moving along with the light. The speed of light in a colinear moving fluid is predicted accurately by the colinear case of the relativistic formula.
 and
and 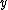 axes, it is convenient to use the same units for space and time, otherwise there is a unit conversion factor which converts incessantly between the units. This conversion factor is the speed of light
axes, it is convenient to use the same units for space and time, otherwise there is a unit conversion factor which converts incessantly between the units. This conversion factor is the speed of light
, which turns time intervals measured in seconds to lengths measured in meters. In a system where lengths and times are measured in the same units, the speed of light is dimensionless and equal to 1. All velocities are then fractions of the speed of light. To translate to engineering units, replace with
with 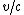 everywhere.
everywhere.
To find the relativistic transformation law, it is useful to introduce the four-velocities and
and
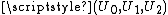 . The four-velocity is defined to be a four vector with relativistic length equal to
. The four-velocity is defined to be a four vector with relativistic length equal to
1 tangent to the space-time path of the object. It is convenient to take the -axis to be the direction of
-axis to be the direction of
motion of the ship, and the -axis so that the
-axis so that the  plane is the plane spanned by the motion of the ship and
plane is the plane spanned by the motion of the ship and
the fly. The ordinary velocity is the ratio of the rate at which the space coordinates are increasing
to the rate at which the time coordinate is increasing:

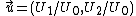
Since the relativistic length of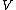 is 1,
is 1, 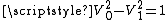 . So
. So  and
and
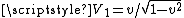 . The Lorentz transformation
. The Lorentz transformation
matrix which boosts the rest frame to
four-velocity is then:
is then:

This matrix rotates the a pure time-axis vector to
to  , and all its columns are relativistically
, and all its columns are relativistically
perpendicular to one another, so it defines a Lorentz transformation.
If a fly is moving with four-velocity in the rest frame, and it is boosted by multiplying by the
in the rest frame, and it is boosted by multiplying by the
matrix above, the new four-velocity is :
:

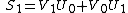

Dividing by the time component and replacing the four-vectors for
and replacing the four-vectors for 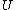 and
and 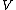 by the
by the
three vectors and
and  gives the relativistic composition law:
gives the relativistic composition law:

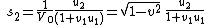
The form of the relativistic composition law can be understood as an effect of the failure of simultaneity
at a distance. For the parallel component, the time dilation decreases the speed, the length contraction
increase it, and the two effects cancel out. The failure of simultaneity means that the fly is changing
simultaneity slices as the projection of onto
onto  . Since this effect is entirely due to the time slicing,
. Since this effect is entirely due to the time slicing,
the same factor multiplies the perpendicular component, but for the perpendicular component there is
no length contraction, so the time dilation adds a factor of .
.
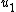 with the component of
with the component of 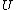 parallel to
parallel to 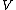 :
:

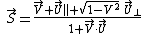
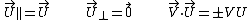

and, expressed in terms of the speeds:
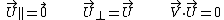
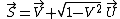
and, expressed in terms of the speeds: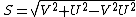
General case (engineering units, replaced
In the general case, the relativistic sum of two velocities  and
and  is given by
is given by
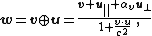
where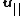 and
and  are the components of
are the components of 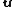 parallel and perpendicular, respectively, to
parallel and perpendicular, respectively, to  , and
, and
 is
is  the reciprocal of the gamma factor
the reciprocal of the gamma factor  .
.
If there is now put as before,

the equation may easily be transformed to the form used by Ungar

Using coordinates this becomes:

where .
.
Einstein velocity addition is commutative only when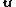 and
and  are parallel. In fact
are parallel. In fact

Also it is not associative and
where gyr is the mathematical abstraction of Thomas precession
into an operator called Thomas gyration and given by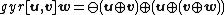
for all w.
The gyr operator forms the foundation of gyrovector space
s.
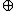 v ≠ v
v ≠ v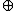 u this raises the question as to which velocity is the real velocity. The paradox is resolved as follows. There are two types of Lorentz transformation
u this raises the question as to which velocity is the real velocity. The paradox is resolved as follows. There are two types of Lorentz transformation
: boosts which correspond to a change in velocity, and rotations. The outcome of a boost followed by another boost is not a pure boost but a boost followed by or preceded by a rotation (Thomas precession
). So unlike Galilean composite transformations, in special relativity, boost composition is parameterized not by velocities alone, but by velocities and orientations, so u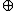 v and v
v and v u both describe correctly but partially the boost composition B(u)B(v).
u both describe correctly but partially the boost composition B(u)B(v).
If the 3x3 matrix form of the rotation applied to 3-coordinates is given by gyr[u,v], then the 4x4 matrix rotation applied to 4-coordinates is given by: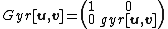 .
.
If B(u)B(v) is parameterized by u v, the rotation Gyr[u,v] associated with the composite boost B(u)B(v) is applied before the boost B(u
v, the rotation Gyr[u,v] associated with the composite boost B(u)B(v) is applied before the boost B(u v), whereas if B(u)B(v) is parameterized by v
v), whereas if B(u)B(v) is parameterized by v u, the boost B(v
u, the boost B(v u) of v
u) of v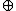 u is followed by the rotation Gyr[u,v], so we get:
u is followed by the rotation Gyr[u,v], so we get: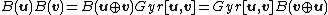 ,
,
In the above, a boost can be represented as a 4x4 matrix. The boost matrix B(v) means the boost B that uses the components of v, i.e. v1, v2, v3 in the entries of the matrix, or rather the components of v/c in the representation that is used in the section Lorentz transformation#Matrix form. The matrix entries depend on the components of the 3-velocity v, and that's what the notation B(v) means. It could be argued that the entries depend on the components of the 4-velocity because 3 of the entries of the 4-velocity are the same as the entries of the 3-velocity, but the usefulness of parameterizing the boost by 3-velocity is that the resultant boost you get from the composition of two boosts uses the components of the 3-velocity composition u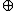 v in the 4x4 matrix B(u
v in the 4x4 matrix B(u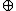 v).
v).
. When the source of a wave is moving with nonrelativistic velocity toward the receiver, the frequency of the waves is increased by a factor of
toward the receiver, the frequency of the waves is increased by a factor of  . If the receiver is moving with velocity
. If the receiver is moving with velocity  , the frequency of the waves detected is decreased by a factor of
, the frequency of the waves detected is decreased by a factor of  . When both the source and the receiver are moving, the frequency measured is given by:
. When both the source and the receiver are moving, the frequency measured is given by:

If a receiver measures velocities using Doppler shifts, and it determines that an object coming towards it is moving with velocity , it is actually determining the shift in frequency, from which it calculates the velocity. Suppose that the receiver itself is moving with velocity
, it is actually determining the shift in frequency, from which it calculates the velocity. Suppose that the receiver itself is moving with velocity  , but it does not take this into account in the calculation. It calculates the value
, but it does not take this into account in the calculation. It calculates the value  falsely assuming that it is at rest. The velocity
falsely assuming that it is at rest. The velocity  can then be thought of as the inferred velocity relative to the ship from Doppler shifts alone. What, then, is the actual velocity of the object relative to the medium?
can then be thought of as the inferred velocity relative to the ship from Doppler shifts alone. What, then, is the actual velocity of the object relative to the medium?
Since the ship determined from the frequency, the frequency shift factor relative to the ship is
from the frequency, the frequency shift factor relative to the ship is

But this factor is not the frequency shift relative to a stationary receiver. For a stationary observer, it must be corrected by dividing by the frequency shift of the ship:
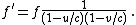
The velocity of the object relative to the medium is then given by

This is the true velocity of the object. Unlike the relativistic addition formula, the velocity is not the physical velocity of the object.
is not the physical velocity of the object.
There is a group of transformations in one space and one time dimension for which this operation forms the addition law. The group is defined by all matrices:
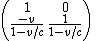
When they act on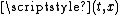 , they produce the transformations
, they produce the transformations
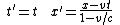
which is a Galilean boost accompanied by a rescaling of the coordinate. When two of these matrices are multiplied, the quantity
coordinate. When two of these matrices are multiplied, the quantity  (the velocity of the frame), combines according to the Doppler addition law.
(the velocity of the frame), combines according to the Doppler addition law.
The physical meaning can be extracted from the transformation. Time is the same for both frames, but the rescaling of the axis keeps the right-moving speed of sound fixed in the moving frame. This means that if the ship uses this transformation to define its frame, the ruler that it uses is the distance that the waves move to the right in one unit of time. The velocity
axis keeps the right-moving speed of sound fixed in the moving frame. This means that if the ship uses this transformation to define its frame, the ruler that it uses is the distance that the waves move to the right in one unit of time. The velocity  can now be given a physical interpretation, although an unusual one. It is the velocity of the object as measured from the ship using a Doppler contracted ruler.
can now be given a physical interpretation, although an unusual one. It is the velocity of the object as measured from the ship using a Doppler contracted ruler.
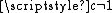 , meaning that the phase velocity of the wave is different from that of light, the relativistic Doppler shift formula does not depend only on the relative velocities of the emitter and receiver, but on their velocities with respect to the medium.
, meaning that the phase velocity of the wave is different from that of light, the relativistic Doppler shift formula does not depend only on the relative velocities of the emitter and receiver, but on their velocities with respect to the medium.
In the rest frame of the medium, the frequency emitted by a relativistic source moving with velocity is decreased by the time dilation of the source:
is decreased by the time dilation of the source: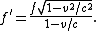
If the receiver is moving with a velocity through the fluid perpendicular to the wave fronts, the frequency received is determined by the proper time
through the fluid perpendicular to the wave fronts, the frequency received is determined by the proper time
between the events where the receiver crosses crests. The fluid frame time between crest-crossings does not require changing frames and is the same as in the nonrelativistic case: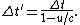
In this time, the receiver has moved (in the fluid frame) an amount
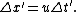
And the proper time between the two crest crossing is
And this is the time between crest-crossings as measured by the receiver. From this, the received frequency can be read off: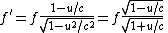
Multiplying the two factors for the emitter and receiver gives the relativistic Doppler shift:

When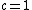 , it simplifies:
, it simplifies:

and then

so that the relativistic Doppler shift of light is determined by the relativistic difference of the two velocities.
It is also possible to determine, in the relativistic case, the actual velocity of a source, when a moving ship falsely determines it from a Doppler shift without taking its own motion into account. Just as in the non-relativistic case, this is the velocity at which a source would have to be moving in order to make the Doppler shift factor for a moving receiver equal to the Doppler shift factor for the velocity . It is the solution of the equation:
. It is the solution of the equation:
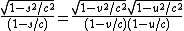
This is the relativistic analog of the Doppler velocity addition formula. When is not the speed of light, the velocity
is not the speed of light, the velocity  is not the velocity of anything, just a false inferred velocity from the point of view of the moving ship. In the relativistic case, there is no group of transformations for which this is the velocity addition law, since it is impossible to independently rescale time and distance measurements.
is not the velocity of anything, just a false inferred velocity from the point of view of the moving ship. In the relativistic case, there is no group of transformations for which this is the velocity addition law, since it is impossible to independently rescale time and distance measurements.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, a velocity-addition formula is an equation that relates the velocities of moving objects in different reference frame
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
s.
Galilean addition of velocities
As GalileoGalileo's ship
Galileo's ship is a physics experiment proposed by Galileo Galilei, the famous 16th and 17th century physicist, astronomer, and philosopher. The experiment was created to disprove popular arguments against the idea of a rotating Earth.-Background:...
observed, if a ship is moving relative to the shore at velocity
 , and a fly is moving with velocity
, and a fly is moving with velocity 
as measured on the ship, calculating the velocity of the fly as measured on the shore is what is meant by the addition of the velocities
 and
and  . When both the fly and the ship are moving slowly compared to light, it is accurate enough to use the vector sum
. When both the fly and the ship are moving slowly compared to light, it is accurate enough to use the vector sum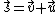
where
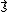 is the velocity of the fly relative to the shore.
is the velocity of the fly relative to the shore.Special theory of relativity
According to the theory of special relativitySpecial relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, the frame of the ship has a different clock rate and distance measure, and the notion of simultaneity in the direction of motion is altered, so the addition law for velocities is changed. This change isn't noticeable at low velocities but as the velocity increases towards the speed of light it becomes important. The addition law is also called a composition law for velocities. For collinear motions, the velocity of the fly relative to the shore is given by
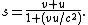
This is also the law of addition of hyperbolic tangents
Hyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
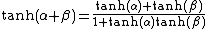
where
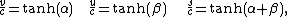
which shows that the composition of collinear velocities is associative and commutative. The quantities
 and
and  are called rapidities
are called rapiditiesRapidity
In relativity, rapidity is an alternative to speed as a framework for measuring motion. On parallel velocities rapidities are simply additive, unlike speeds at relativistic velocities. For low speeds, rapidity and speed are proportional, but for high speeds, rapidity takes a larger value. The...
. The reason that the velocities are hyperbolic tangents is because the Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
can be thought of as the application of a hyperbolic rotation through a hyperbolic angle
Hyperbolic angle
In mathematics, a hyperbolic angle is a geometric figure that divides a hyperbola. The science of hyperbolic angle parallels the relation of an ordinary angle to a circle...
which is the rapidity
Rapidity
In relativity, rapidity is an alternative to speed as a framework for measuring motion. On parallel velocities rapidities are simply additive, unlike speeds at relativistic velocities. For low speeds, rapidity and speed are proportional, but for high speeds, rapidity takes a larger value. The...
. Suppose the velocity of a line in space-time is the slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of the line, which is the hyperbolic tangent of the rapidity, just as the slope of the
 -axis after a rotation is given by the tangent of the rotation angle. When a plane is successively rotated by two angles, the final rotation is by the sum of the two angles. So the final slope of the
-axis after a rotation is given by the tangent of the rotation angle. When a plane is successively rotated by two angles, the final rotation is by the sum of the two angles. So the final slope of the  -axis is the tangent of the sum of the two angles. In the same way, the slope of the time axis after two boosts is the hyperbolic tangent of the sum of the two rapidities.
-axis is the tangent of the sum of the two angles. In the same way, the slope of the time axis after two boosts is the hyperbolic tangent of the sum of the two rapidities.The colinear law of composition of velocities gave the first test of the kinematics of the special theory of relativity. Using a Michelson interferometer
Michelson interferometer
The Michelson interferometer is the most common configuration for optical interferometry and was invented by Albert Abraham Michelson. An interference pattern is produced by splitting a beam of light into two paths, bouncing the beams back and recombining them...
, Fizeau
Hippolyte Fizeau
Armand Hippolyte Louis Fizeau was a French physicist.-Biography:Fizeau was born in Paris. His earliest work was concerned with improvements in photographic processes. Following suggestions by François Arago, Léon Foucault and Fizeau collaborated in a series of investigations on the interference of...
measured
Fizeau experiment
The Fizeau experiment was carried out by Hippolyte Fizeau in 1851 to measure the relative speeds of light in moving water. Albert Einstein later pointed out the importance of the experiment for special relativity...
the speed of light in a fluid moving parallel to the light. The speed of
light in the fluid is slower than the speed of light in vacuum, and it changes if the fluid is moving along with the light. The speed of light in a colinear moving fluid is predicted accurately by the colinear case of the relativistic formula.
Derivation
Since a relativistic transformation rotates space and time into each other much as geometric rotations in the plane rotate the and
and 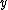 axes, it is convenient to use the same units for space and time, otherwise there is a unit conversion factor which converts incessantly between the units. This conversion factor is the speed of light
axes, it is convenient to use the same units for space and time, otherwise there is a unit conversion factor which converts incessantly between the units. This conversion factor is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
, which turns time intervals measured in seconds to lengths measured in meters. In a system where lengths and times are measured in the same units, the speed of light is dimensionless and equal to 1. All velocities are then fractions of the speed of light. To translate to engineering units, replace
 with
with 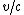 everywhere.
everywhere.To find the relativistic transformation law, it is useful to introduce the four-velocities
 and
and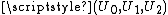 . The four-velocity is defined to be a four vector with relativistic length equal to
. The four-velocity is defined to be a four vector with relativistic length equal to1 tangent to the space-time path of the object. It is convenient to take the
 -axis to be the direction of
-axis to be the direction ofmotion of the ship, and the
 -axis so that the
-axis so that the  plane is the plane spanned by the motion of the ship and
plane is the plane spanned by the motion of the ship andthe fly. The ordinary velocity is the ratio of the rate at which the space coordinates are increasing
to the rate at which the time coordinate is increasing:

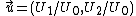
Since the relativistic length of
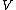 is 1,
is 1, 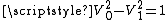 . So
. So  and
and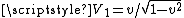 . The Lorentz transformation
. The Lorentz transformationLorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
matrix which boosts the rest frame to
four-velocity
 is then:
is then:
This matrix rotates the a pure time-axis vector
 to
to  , and all its columns are relativistically
, and all its columns are relativisticallyperpendicular to one another, so it defines a Lorentz transformation.
If a fly is moving with four-velocity
 in the rest frame, and it is boosted by multiplying by the
in the rest frame, and it is boosted by multiplying by thematrix above, the new four-velocity is
 :
:
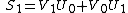

Dividing by the time component
 and replacing the four-vectors for
and replacing the four-vectors for 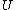 and
and 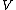 by the
by thethree vectors
 and
and  gives the relativistic composition law:
gives the relativistic composition law:
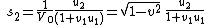
The form of the relativistic composition law can be understood as an effect of the failure of simultaneity
at a distance. For the parallel component, the time dilation decreases the speed, the length contraction
increase it, and the two effects cancel out. The failure of simultaneity means that the fly is changing
simultaneity slices as the projection of
 onto
onto  . Since this effect is entirely due to the time slicing,
. Since this effect is entirely due to the time slicing,the same factor multiplies the perpendicular component, but for the perpendicular component there is
no length contraction, so the time dilation adds a factor of
 .
.Vector notation
To translate the formula of the previous section to three-vector notation, replace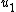 with the component of
with the component of 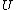 parallel to
parallel to 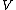 :
:General case

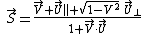
Special case: parallel velocities
In the case where the velocities are parallel we have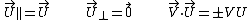

and, expressed in terms of the speeds:

Special case: orthogonal velocities
In the case where the velocities are orthogonal we have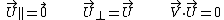
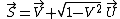
and, expressed in terms of the speeds:
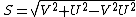
General case (engineering units, replaced  with v / c )
with v / c )
In the general case, the relativistic sum of two velocities  and
and  is given by
is given by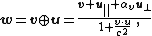
where
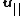 and
and  are the components of
are the components of 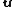 parallel and perpendicular, respectively, to
parallel and perpendicular, respectively, to  , and
, and is
is  the reciprocal of the gamma factor
the reciprocal of the gamma factor  .
.If there is now put as before,

the equation may easily be transformed to the form used by Ungar

Using coordinates this becomes:

where
 .
.Einstein velocity addition is commutative only when
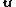 and
and  are parallel. In fact
are parallel. In fact
Also it is not associative and

where gyr is the mathematical abstraction of Thomas precession
Thomas precession
In physics the Thomas precession, named after Llewellyn Thomas, is a special relativistic correction that applies to the spin of an elementary particle or the rotation of a macroscopic gyroscope and relates the angular velocity of the spin of a particle following a curvilinear orbit to the angular...
into an operator called Thomas gyration and given by
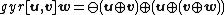
for all w.
The gyr operator forms the foundation of gyrovector space
Gyrovector space
A gyrovector space is a mathematical concept for studying hyperbolic geometry in analogy to the way vector spaces are used in Euclidean geometry. This vector-based approach has been developed by Abraham Albert Ungar from the late 1980s onwards...
s.
Velocity composition paradox
Since in general u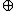 v ≠ v
v ≠ v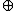 u this raises the question as to which velocity is the real velocity. The paradox is resolved as follows. There are two types of Lorentz transformation
u this raises the question as to which velocity is the real velocity. The paradox is resolved as follows. There are two types of Lorentz transformationLorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
: boosts which correspond to a change in velocity, and rotations. The outcome of a boost followed by another boost is not a pure boost but a boost followed by or preceded by a rotation (Thomas precession
Thomas precession
In physics the Thomas precession, named after Llewellyn Thomas, is a special relativistic correction that applies to the spin of an elementary particle or the rotation of a macroscopic gyroscope and relates the angular velocity of the spin of a particle following a curvilinear orbit to the angular...
). So unlike Galilean composite transformations, in special relativity, boost composition is parameterized not by velocities alone, but by velocities and orientations, so u
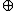 v and v
v and v u both describe correctly but partially the boost composition B(u)B(v).
u both describe correctly but partially the boost composition B(u)B(v).If the 3x3 matrix form of the rotation applied to 3-coordinates is given by gyr[u,v], then the 4x4 matrix rotation applied to 4-coordinates is given by:
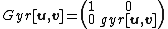 .
.If B(u)B(v) is parameterized by u
 v, the rotation Gyr[u,v] associated with the composite boost B(u)B(v) is applied before the boost B(u
v, the rotation Gyr[u,v] associated with the composite boost B(u)B(v) is applied before the boost B(u v), whereas if B(u)B(v) is parameterized by v
v), whereas if B(u)B(v) is parameterized by v u, the boost B(v
u, the boost B(v u) of v
u) of v u is followed by the rotation Gyr[u,v], so we get:
u is followed by the rotation Gyr[u,v], so we get: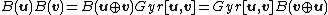 ,
,In the above, a boost can be represented as a 4x4 matrix. The boost matrix B(v) means the boost B that uses the components of v, i.e. v1, v2, v3 in the entries of the matrix, or rather the components of v/c in the representation that is used in the section Lorentz transformation#Matrix form. The matrix entries depend on the components of the 3-velocity v, and that's what the notation B(v) means. It could be argued that the entries depend on the components of the 4-velocity because 3 of the entries of the 4-velocity are the same as the entries of the 3-velocity, but the usefulness of parameterizing the boost by 3-velocity is that the resultant boost you get from the composition of two boosts uses the components of the 3-velocity composition u
 v in the 4x4 matrix B(u
v in the 4x4 matrix B(u v).
v).Doppler shift
A notion of velocity addition can also be formulated in the theory of the nonrelativistic, one dimensional Doppler shiftDoppler effect
The Doppler effect , named after Austrian physicist Christian Doppler who proposed it in 1842 in Prague, is the change in frequency of a wave for an observer moving relative to the source of the wave. It is commonly heard when a vehicle sounding a siren or horn approaches, passes, and recedes from...
. When the source of a wave is moving with nonrelativistic velocity
 toward the receiver, the frequency of the waves is increased by a factor of
toward the receiver, the frequency of the waves is increased by a factor of  . If the receiver is moving with velocity
. If the receiver is moving with velocity  , the frequency of the waves detected is decreased by a factor of
, the frequency of the waves detected is decreased by a factor of  . When both the source and the receiver are moving, the frequency measured is given by:
. When both the source and the receiver are moving, the frequency measured is given by:
If a receiver measures velocities using Doppler shifts, and it determines that an object coming towards it is moving with velocity
 , it is actually determining the shift in frequency, from which it calculates the velocity. Suppose that the receiver itself is moving with velocity
, it is actually determining the shift in frequency, from which it calculates the velocity. Suppose that the receiver itself is moving with velocity  , but it does not take this into account in the calculation. It calculates the value
, but it does not take this into account in the calculation. It calculates the value  falsely assuming that it is at rest. The velocity
falsely assuming that it is at rest. The velocity  can then be thought of as the inferred velocity relative to the ship from Doppler shifts alone. What, then, is the actual velocity of the object relative to the medium?
can then be thought of as the inferred velocity relative to the ship from Doppler shifts alone. What, then, is the actual velocity of the object relative to the medium?Since the ship determined
 from the frequency, the frequency shift factor relative to the ship is
from the frequency, the frequency shift factor relative to the ship is
But this factor is not the frequency shift relative to a stationary receiver. For a stationary observer, it must be corrected by dividing by the frequency shift of the ship:
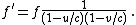
The velocity of the object relative to the medium is then given by

This is the true velocity of the object. Unlike the relativistic addition formula, the velocity
 is not the physical velocity of the object.
is not the physical velocity of the object.There is a group of transformations in one space and one time dimension for which this operation forms the addition law. The group is defined by all matrices:
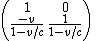
When they act on
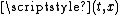 , they produce the transformations
, they produce the transformations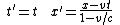
which is a Galilean boost accompanied by a rescaling of the
 coordinate. When two of these matrices are multiplied, the quantity
coordinate. When two of these matrices are multiplied, the quantity  (the velocity of the frame), combines according to the Doppler addition law.
(the velocity of the frame), combines according to the Doppler addition law.The physical meaning can be extracted from the transformation. Time is the same for both frames, but the rescaling of the
 axis keeps the right-moving speed of sound fixed in the moving frame. This means that if the ship uses this transformation to define its frame, the ruler that it uses is the distance that the waves move to the right in one unit of time. The velocity
axis keeps the right-moving speed of sound fixed in the moving frame. This means that if the ship uses this transformation to define its frame, the ruler that it uses is the distance that the waves move to the right in one unit of time. The velocity  can now be given a physical interpretation, although an unusual one. It is the velocity of the object as measured from the ship using a Doppler contracted ruler.
can now be given a physical interpretation, although an unusual one. It is the velocity of the object as measured from the ship using a Doppler contracted ruler.Relativistic Doppler shift
In the theory of the relativistic Doppler shift, the case where the speed of the wave is equal to the speed of light is special, because then there is no preferred rest-frame. In this case the frequency of the received waves can only depend on the relativistic sum of the velocities of the emitter and the receiver. But when the speed of the wave , meaning that the phase velocity of the wave is different from that of light, the relativistic Doppler shift formula does not depend only on the relative velocities of the emitter and receiver, but on their velocities with respect to the medium.
, meaning that the phase velocity of the wave is different from that of light, the relativistic Doppler shift formula does not depend only on the relative velocities of the emitter and receiver, but on their velocities with respect to the medium.In the rest frame of the medium, the frequency emitted by a relativistic source moving with velocity
 is decreased by the time dilation of the source:
is decreased by the time dilation of the source: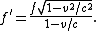
If the receiver is moving with a velocity
 through the fluid perpendicular to the wave fronts, the frequency received is determined by the proper time
through the fluid perpendicular to the wave fronts, the frequency received is determined by the proper timeMinkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
between the events where the receiver crosses crests. The fluid frame time between crest-crossings does not require changing frames and is the same as in the nonrelativistic case:
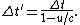
In this time, the receiver has moved (in the fluid frame) an amount
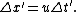
And the proper time between the two crest crossing is

And this is the time between crest-crossings as measured by the receiver. From this, the received frequency can be read off:
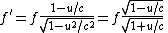
Multiplying the two factors for the emitter and receiver gives the relativistic Doppler shift:

When
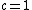 , it simplifies:
, it simplifies:
and then

so that the relativistic Doppler shift of light is determined by the relativistic difference of the two velocities.
It is also possible to determine, in the relativistic case, the actual velocity of a source, when a moving ship falsely determines it from a Doppler shift without taking its own motion into account. Just as in the non-relativistic case, this is the velocity at which a source would have to be moving in order to make the Doppler shift factor for a moving receiver equal to the Doppler shift factor for the velocity
 . It is the solution of the equation:
. It is the solution of the equation: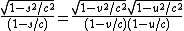
This is the relativistic analog of the Doppler velocity addition formula. When
 is not the speed of light, the velocity
is not the speed of light, the velocity  is not the velocity of anything, just a false inferred velocity from the point of view of the moving ship. In the relativistic case, there is no group of transformations for which this is the velocity addition law, since it is impossible to independently rescale time and distance measurements.
is not the velocity of anything, just a false inferred velocity from the point of view of the moving ship. In the relativistic case, there is no group of transformations for which this is the velocity addition law, since it is impossible to independently rescale time and distance measurements.External links
- Sommerfeld, Arnold (1909): On the Composition of Velocities in the Theory of Relativity, Verh. der DPG, 21: 577-582

