
Vertex enumeration problem
Encyclopedia
In mathematics, the vertex enumeration problem for a polytope
, a polyhedral cell complex, a hyperplane arrangement, or some other object of discrete geometry
, is the problem of determination of the object's vertices
given some formal representation of the object. A classical example is the problem of enumeration of the vertices of a convex polytope
specified by a set of linear inequalities: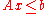
where A is an m×n matrix, x is an n×1 column vector of variables, and b is an m×1 column vector of constants.
of the problem is a subject of research in computer science
.
A 1992 article by David Avis
and Komei Fukuda presents an algorithm which finds the v vertices of a polytope defined by a nondegenerate system of n inequalities in d dimensions (or, dually, the v facet
s of the convex hull
of n points in d dimensions, where each facet contains exactly d given points) in time O(ndv) and space O(nd). The v vertices in a simple arrangement of n hyperplane
s in d dimensions can be found in O(n2dv) time and O(nd) space complexity. The Avis–Fukuda algorithm adapted the criss-cross algorithm
for oriented matroids.
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
, a polyhedral cell complex, a hyperplane arrangement, or some other object of discrete geometry
Discrete geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles,...
, is the problem of determination of the object's vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
given some formal representation of the object. A classical example is the problem of enumeration of the vertices of a convex polytope
Convex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
specified by a set of linear inequalities:
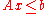
where A is an m×n matrix, x is an n×1 column vector of variables, and b is an m×1 column vector of constants.
Computational complexity
The computational complexityComputational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
of the problem is a subject of research in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
.
A 1992 article by David Avis
David Avis
David Michael Avis is a Canadian and British computer scientist known for his contributions to geometric computations. Avis is a professor in computational geometry and applied mathematics in the School of Computer Science, McGill University, in Montreal.Avis received his Ph.D. in 1977 from...
and Komei Fukuda presents an algorithm which finds the v vertices of a polytope defined by a nondegenerate system of n inequalities in d dimensions (or, dually, the v facet
Facet
Facets are flat faces on geometric shapes. The organization of naturally occurring facets was key to early developments in crystallography, since they reflect the underlying symmetry of the crystal structure...
s of the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of n points in d dimensions, where each facet contains exactly d given points) in time O(ndv) and space O(nd). The v vertices in a simple arrangement of n hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
s in d dimensions can be found in O(n2dv) time and O(nd) space complexity. The Avis–Fukuda algorithm adapted the criss-cross algorithm
Criss-cross algorithm
In mathematical optimization, the criss-cross algorithm denotes a family of algorithms for linear programming. Variants of the criss-cross algorithm also solve more general problems with linear inequality constraints and nonlinear objective functions; there are criss-cross algorithms for...
for oriented matroids.

