
Vertex model
Encyclopedia
A vertex model is a type of statistical mechanics
model
in which the Boltzmann weight
s are associated with a vertex
in the model (representing an atom
or particle). This contrasts with a nearest-neighbour model, such as the Ising model
, in which the energy, and thus the Boltzmann weight of a statistical microstate is attributed to the bonds connecting two neighbouring particles. The energy associated with a vertex in the lattice of particles is thus dependent on the state of the bonds which connect it to adjacent vertices. It turns out that every solution of the Yang-Baxter equation
with spectral parameters in a tensor product of vector space
s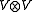 yields an exactly-solvable vertex model.
yields an exactly-solvable vertex model.
 Although the model can be applied to various geometries
Although the model can be applied to various geometries
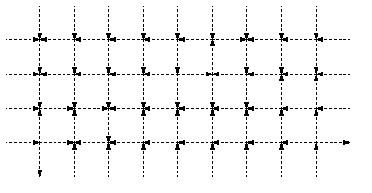
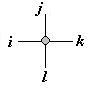
in any number of dimensions, with any number of possible states for a given bond, the most fundamental examples occur for two dimensional lattices, the simplest being a square lattice
where each bond has two possible states. In this model, every particle is connected to four other particles, and each of the four bonds adjacent to the particle has two possible states, indicated by the direction of an arrow on the bond. In this model, each vertex can adopt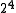 possible configurations. The energy
possible configurations. The energy
for a given vertex can be given by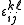 ,
,
 with a state of the lattice is an assignment of a state of each bond, with the total energy of the state being the sum of the vertex energies. As the energy is often divergent for an infinite lattice, the model is studied for a finite lattice as the lattice approaches infinite size. Periodic
with a state of the lattice is an assignment of a state of each bond, with the total energy of the state being the sum of the vertex energies. As the energy is often divergent for an infinite lattice, the model is studied for a finite lattice as the lattice approaches infinite size. Periodic
or domain wall boundary conditions may be imposed on the model.
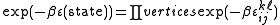
where the Boltzmann weights for the vertices are written
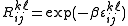 .
.
The probability
of the system being in any given state at a particular time, and hence the properties of the system are determined by the partition function
, for which an analytic solution is desired.
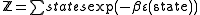
where β=1/kT, T is temperature
and k is Boltzmann's constant. The probability that the system is in any given microstate
is given by
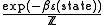
so that the average value of the energy of the system is given by
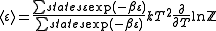
In order to evaluate the partition function, firstly examine the states of a row of vertices.
 The external edges are free variables, with summation over the internal bonds. Hence, form the row partition function
The external edges are free variables, with summation over the internal bonds. Hence, form the row partition function
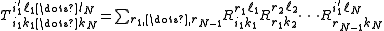
This can be reformulated in terms of an auxiliary n-dimensional vector space V, with a basis
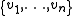 , and
, and 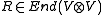 as
as
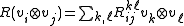
and as
as
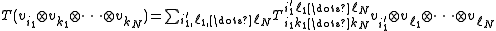
thereby implying that T can be written as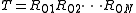
where the indices indicate the factors of the tensor product
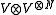 on which R operates. Summing over the states of the bonds in the first row with the periodic boundary conditions
on which R operates. Summing over the states of the bonds in the first row with the periodic boundary conditions 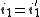 , gives
, gives
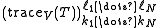
where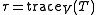 is the row-transfer matrix.
is the row-transfer matrix.
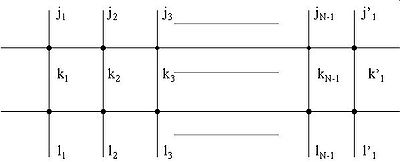 By summing the contributions over two rows, the result is
By summing the contributions over two rows, the result is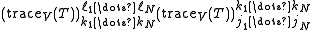
which upon summation over the vertical bonds connecting the first two rows gives: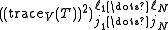
for M rows, this gives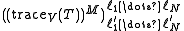
and then applying the periodic boundary conditions to the vertical columns, the partition function can be expressed in terms of the transfer matrix as
as
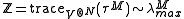
where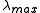 is the largest eigenvalue of
is the largest eigenvalue of  . The approximation follows from the fact that the eigenvalues of
. The approximation follows from the fact that the eigenvalues of 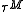 are the eigenvalues of
are the eigenvalues of  to the power of M, and as
to the power of M, and as 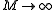 , the power of the largest eigenvalue becomes much larger than the others. As the trace
, the power of the largest eigenvalue becomes much larger than the others. As the trace
is the sum of the eigenvalues, the problem of calculating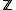 reduces to the problem of finding the maximum eigenvalue of
reduces to the problem of finding the maximum eigenvalue of  . This in it itself is another field of study. However, a standard approach to the problem of finding the largest eigenvalue of
. This in it itself is another field of study. However, a standard approach to the problem of finding the largest eigenvalue of  is to find a large family of operators which commute with
is to find a large family of operators which commute with  . This implies that the eigenspaces are common, and restricts the possible space of solutions. Such a family of commuting operators is usually found by means of the Yang-Baxter equation
. This implies that the eigenspaces are common, and restricts the possible space of solutions. Such a family of commuting operators is usually found by means of the Yang-Baxter equation
, which thus relates statistical mechanics to the study of quantum group
s.
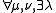 such that
such that
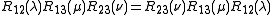
This is a parameterized version of the Yang-Baxter equation, corresponding to the possible dependence of the vertex energies,and hence the Boltzmann weights R on external parameters, such as temperature, external fields, etc.
The integrability condition implies the following relation.
Proposition: For an integrable vertex model, with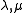 and
and  defined as above, then
defined as above, then
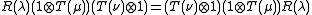
as endomorphism
s of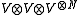 , where
, where 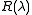 acts on the first two vectors of the tensor product.
acts on the first two vectors of the tensor product.
It follows by multiplying both sides of the above equation on the right by and using the cyclic property of the trace operator that the following corollary holds.
and using the cyclic property of the trace operator that the following corollary holds.
Corollary: For an integrable vertex model for which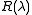 is invertible
is invertible 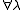 , the transfer matrix
, the transfer matrix 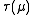 commutes with
commutes with 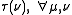 .
.
This illustrates the role of the Yang-Baxter equation in the solution of solvable lattice models. Since the transfer matrices commute for all
commute for all 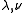 , the eigenvectors of
, the eigenvectors of  are common, and hence independent of the parameterization. It is a recurring theme which appears in many other types of statistical mechanical models to look for these commuting transfer matrices.
are common, and hence independent of the parameterization. It is a recurring theme which appears in many other types of statistical mechanical models to look for these commuting transfer matrices.
From the definition of R above, it follows that for every solution of the Yang-Baxter equation in the tensor product of two n-dimensional vector spaces, there is a corresponding 2-dimensional solvable vertex model where each of the bonds can be in the possible states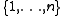 , where R is an endomorphism in the space spanned by
, where R is an endomorphism in the space spanned by 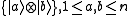 . This motivates the classification of all the finite-dimensional irreducible representations
. This motivates the classification of all the finite-dimensional irreducible representations
of a given Quantum algebra
in order to find solvable models coreesponding to it.
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
model
Model (physical)
A physical model is a smaller or larger physical copy of an object...
in which the Boltzmann weight
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
s are associated with a vertex
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
in the model (representing an atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
or particle). This contrasts with a nearest-neighbour model, such as the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
, in which the energy, and thus the Boltzmann weight of a statistical microstate is attributed to the bonds connecting two neighbouring particles. The energy associated with a vertex in the lattice of particles is thus dependent on the state of the bonds which connect it to adjacent vertices. It turns out that every solution of the Yang-Baxter equation
Yang-Baxter equation
The Yang–Baxter equation is an equation which was first introduced in the field of statistical mechanics. It takes its name from independent work of C. N. Yang from 1968, and R. J. Baxter from 1971...
with spectral parameters in a tensor product of vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s
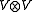 yields an exactly-solvable vertex model.
yields an exactly-solvable vertex model.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
in any number of dimensions, with any number of possible states for a given bond, the most fundamental examples occur for two dimensional lattices, the simplest being a square lattice
Square lattice
In mathematics, the square lattice is a type of lattice in a two-dimensional Euclidean space. It is the two-dimensional version of the integer lattice. It is one of the five types of two-dimensional lattices as classified by their symmetry groups; its symmetry group is known symbolically as p4m.Two...
where each bond has two possible states. In this model, every particle is connected to four other particles, and each of the four bonds adjacent to the particle has two possible states, indicated by the direction of an arrow on the bond. In this model, each vertex can adopt
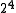 possible configurations. The energy
possible configurations. The energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
for a given vertex can be given by
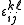 ,
,
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
or domain wall boundary conditions may be imposed on the model.
Discussion
For a given state, the Boltzmann weight can be written in terms of the product of the Boltzmann weights of the corresponding vertices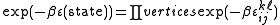
where the Boltzmann weights for the vertices are written
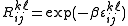 .
.The probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of the system being in any given state at a particular time, and hence the properties of the system are determined by the partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
, for which an analytic solution is desired.
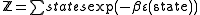
where β=1/kT, T is temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
and k is Boltzmann's constant. The probability that the system is in any given microstate
Microstate
A microstate or ministate is a sovereign state having a very small population or very small land area, but usually both. Some examples include Liechtenstein, Malta, Monaco, Nauru, Singapore, and Vatican City....
is given by
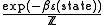
so that the average value of the energy of the system is given by
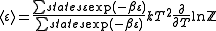
In order to evaluate the partition function, firstly examine the states of a row of vertices.

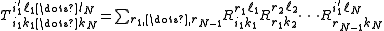
This can be reformulated in terms of an auxiliary n-dimensional vector space V, with a basis
Basis
Basis may refer to* Cost basis, in income tax law, the original cost of property adjusted for factors such as depreciation.* Basis of futures, the value differential between a future and the spot price...
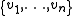 , and
, and 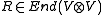 as
as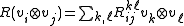
and
 as
as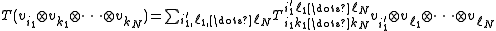
thereby implying that T can be written as
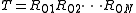
where the indices indicate the factors of the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
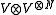 on which R operates. Summing over the states of the bonds in the first row with the periodic boundary conditions
on which R operates. Summing over the states of the bonds in the first row with the periodic boundary conditions 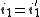 , gives
, gives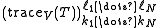
where
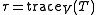 is the row-transfer matrix.
is the row-transfer matrix.
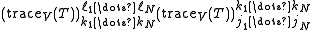
which upon summation over the vertical bonds connecting the first two rows gives:
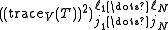
for M rows, this gives
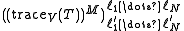
and then applying the periodic boundary conditions to the vertical columns, the partition function can be expressed in terms of the transfer matrix
 as
as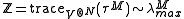
where
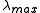 is the largest eigenvalue of
is the largest eigenvalue of  . The approximation follows from the fact that the eigenvalues of
. The approximation follows from the fact that the eigenvalues of 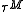 are the eigenvalues of
are the eigenvalues of  to the power of M, and as
to the power of M, and as 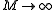 , the power of the largest eigenvalue becomes much larger than the others. As the trace
, the power of the largest eigenvalue becomes much larger than the others. As the traceTrace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
is the sum of the eigenvalues, the problem of calculating
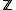 reduces to the problem of finding the maximum eigenvalue of
reduces to the problem of finding the maximum eigenvalue of  . This in it itself is another field of study. However, a standard approach to the problem of finding the largest eigenvalue of
. This in it itself is another field of study. However, a standard approach to the problem of finding the largest eigenvalue of  is to find a large family of operators which commute with
is to find a large family of operators which commute with  . This implies that the eigenspaces are common, and restricts the possible space of solutions. Such a family of commuting operators is usually found by means of the Yang-Baxter equation
. This implies that the eigenspaces are common, and restricts the possible space of solutions. Such a family of commuting operators is usually found by means of the Yang-Baxter equationYang-Baxter equation
The Yang–Baxter equation is an equation which was first introduced in the field of statistical mechanics. It takes its name from independent work of C. N. Yang from 1968, and R. J. Baxter from 1971...
, which thus relates statistical mechanics to the study of quantum group
Quantum group
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
s.
Integrability
Definition: A vertex model is integrable if,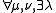 such that
such that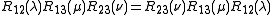
This is a parameterized version of the Yang-Baxter equation, corresponding to the possible dependence of the vertex energies,and hence the Boltzmann weights R on external parameters, such as temperature, external fields, etc.
The integrability condition implies the following relation.
Proposition: For an integrable vertex model, with
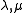 and
and  defined as above, then
defined as above, then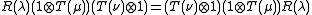
as endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s of
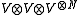 , where
, where 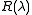 acts on the first two vectors of the tensor product.
acts on the first two vectors of the tensor product.It follows by multiplying both sides of the above equation on the right by
 and using the cyclic property of the trace operator that the following corollary holds.
and using the cyclic property of the trace operator that the following corollary holds.Corollary: For an integrable vertex model for which
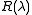 is invertible
is invertible 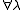 , the transfer matrix
, the transfer matrix 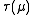 commutes with
commutes with 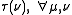 .
.This illustrates the role of the Yang-Baxter equation in the solution of solvable lattice models. Since the transfer matrices
 commute for all
commute for all 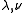 , the eigenvectors of
, the eigenvectors of  are common, and hence independent of the parameterization. It is a recurring theme which appears in many other types of statistical mechanical models to look for these commuting transfer matrices.
are common, and hence independent of the parameterization. It is a recurring theme which appears in many other types of statistical mechanical models to look for these commuting transfer matrices.From the definition of R above, it follows that for every solution of the Yang-Baxter equation in the tensor product of two n-dimensional vector spaces, there is a corresponding 2-dimensional solvable vertex model where each of the bonds can be in the possible states
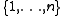 , where R is an endomorphism in the space spanned by
, where R is an endomorphism in the space spanned by 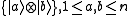 . This motivates the classification of all the finite-dimensional irreducible representations
. This motivates the classification of all the finite-dimensional irreducible representationsRepresentation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of a given Quantum algebra
Quantum algebra
Quantum algebra is one of the top-level mathematics categories used by the arXiv.Subjects include:*Quantum groups*Skein theories*Operadic algebra*Diagrammatic algebra*Quantum field theory-External links:**R. Jagannathan,...
in order to find solvable models coreesponding to it.
Notable vertex models
- Six-vertex model
- Eight-vertex modelEight-vertex modelIn statistical mechanics, the eight-vertex model is a generalisation of the ice-type models; it was discussed by Sutherland, and Fan & Wu, and solved by Baxter in the zero-field case.-Description:...
- Nineteen-vertex model (Izergin-Korepin model)



