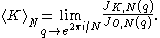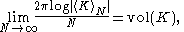Volume conjecture
Encyclopedia
In the branch of mathematics called knot theory
, the volume conjecture is the following open problem that relates quantum invariant
s of knots to the hyperbolic geometry of knot complement
s.
Let O denote the unknot
. For any knot K let be Kashaev's invariant of
be Kashaev's invariant of 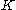 ; this invariant coincides with the following evaluation of the
; this invariant coincides with the following evaluation of the 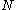 -colored Jones polynomial
-colored Jones polynomial 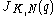 of
of 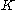 :
:
Then the volume conjecture states that
where vol(K) denotes the hyperbolic volume of the complement of K in the 3-sphere
.
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, the volume conjecture is the following open problem that relates quantum invariant
Quantum invariant
In the mathematical field of knot theory, a quantum invariant of a knot or link is a linear sum of colored Jones polynomial of surgery presentations of the knot complement.-List of invariants:*Finite type invariant*Kontsevich invariant*Kashaev's invariant...
s of knots to the hyperbolic geometry of knot complement
Knot complement
In mathematics, the knot complement of a tame knot K is the complement of the interior of the embedding of a solid torus into the 3-sphere. To make this precise, suppose that K is a knot in a three-manifold M. Let N be a thickened neighborhood of K; so N is a solid torus...
s.
Let O denote the unknot
Unknot
The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...
. For any knot K let
 be Kashaev's invariant of
be Kashaev's invariant of 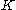 ; this invariant coincides with the following evaluation of the
; this invariant coincides with the following evaluation of the 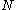 -colored Jones polynomial
-colored Jones polynomial 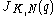 of
of 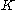 :
:
Then the volume conjecture states that
where vol(K) denotes the hyperbolic volume of the complement of K in the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
.