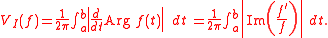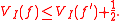Voorhoeve index
Encyclopedia
Rolle's theorem
states that if f is a continuously differentiable real-valued function on the real line, and f(a) = f(b) = 0, where a < b, then its derivative f ' must have a zero strictly between a and b. Or, more generally, if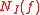
denotes the number of zeros of the continuously differentiable function f on the interval 
, then 
≤ 
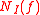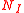(f ') + 1.
The Voorhoeve index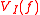
of a complex-valued function f that is analytic in a complex neighbourhood of the real interval 
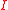= [a, b] is given by
(Different authors use different normalization factors.)
Now one has the analogue of Rolle's theorem:
This leads to bounds on the number of zeros of an analytic function in a complex region.
Rolle's theorem
In calculus, Rolle's theorem essentially states that a differentiable function which attains equal values at two distinct points must have a point somewhere between them where the first derivative is zero.-Standard version of the theorem:If a real-valued function ƒ is continuous on a closed...
states that if f is a continuously differentiable real-valued function on the real line, and f(a) = f(b) = 0, where a < b, then its derivative f ' must have a zero strictly between a and b. Or, more generally, if
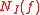denotes the number of zeros of the continuously differentiable function f on the interval , then 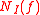≤ 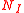(f ') + 1.The Voorhoeve index
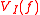of a complex-valued function f that is analytic in a complex neighbourhood of the real interval 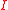= [a, b] is given by
(Different authors use different normalization factors.)
Now one has the analogue of Rolle's theorem:
This leads to bounds on the number of zeros of an analytic function in a complex region.