Waldhausen category
Encyclopedia
In mathematics
a Waldhausen category (after Friedhelm Waldhausen
) is a category
C with a zero object equipped with cofibration
s co(C) and weak equivalences we(C), both containing all isomorphism
s, both compatible with pushout
, and co(C) containing the unique morphisms
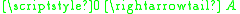
from the zero-object to any object A.
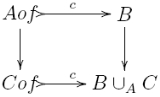
To be more precise about the pushouts, we require when
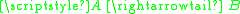
is a cofibration and
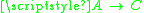
is any map, that we have a push-out
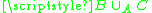
where the map
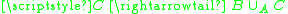
is a cofibration:

A category C is equipped with bifibrations if it has cofibrations and its opposite category COP has so also. In that case, we denote the fibrations of COP by quot(C).
In that case, C is a biWaldhausen category if C has bifibrations and weak equivalences such that both (C, co(C), we) and (COP, quot(C), weOP) are Waldhausen categories.
As examples one may think of exact categories
, where the cofibrations are the admissible monomorphisms. Another example is the full subcategory of bifibrant objects in a pointed model categories
, that is, the full subcategory consisting of those objects for which
for which 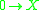 is a cofibration and
is a cofibration and 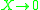 is a fibration.
is a fibration.
Waldhausen and biWaldhausen categories are linked with algebraic K-theory
. There, many interesting categories are complicial biWaldhausen categories. For example:
The category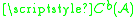 of bounded chaincomplexes on an exact category
of bounded chaincomplexes on an exact category 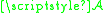
The category of functors
of functors 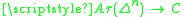 when
when  is so.
is so.
And given a diagram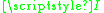 , then
, then  is a nice complicial biWaldhausen category when
is a nice complicial biWaldhausen category when 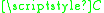 is.
is.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
a Waldhausen category (after Friedhelm Waldhausen
Friedhelm Waldhausen
Friedhelm Waldhausen is a German mathematician known for his work in algebraic topology.-Academic life:...
) is a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
C with a zero object equipped with cofibration
Cofibration
In mathematics, in particular homotopy theory, a continuous mappingi\colon A \to X,where A and X are topological spaces, is a cofibration if it satisfies the homotopy extension property with respect to all spaces Y. The name is because the dual condition, the homotopy lifting property, defines...
s co(C) and weak equivalences we(C), both containing all isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
s, both compatible with pushout
Pushout (category theory)
In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain: it is the colimit of the span X \leftarrow Z \rightarrow Y.The pushout is the...
, and co(C) containing the unique morphisms
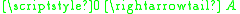
from the zero-object to any object A.
To be more precise about the pushouts, we require when
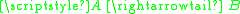
is a cofibration and
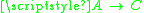
is any map, that we have a push-out
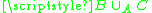
where the map
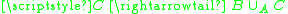
is a cofibration:

A category C is equipped with bifibrations if it has cofibrations and its opposite category COP has so also. In that case, we denote the fibrations of COP by quot(C).
In that case, C is a biWaldhausen category if C has bifibrations and weak equivalences such that both (C, co(C), we) and (COP, quot(C), weOP) are Waldhausen categories.
As examples one may think of exact categories
Exact category
In mathematics, an exact category is a concept of category theory due to Daniel Quillen which is designed to encapsulate the properties of short exact sequences in abelian categories without requiring that morphisms actually possess kernels and cokernels, which is necessary for the usual definition...
, where the cofibrations are the admissible monomorphisms. Another example is the full subcategory of bifibrant objects in a pointed model categories
Model category
In mathematics, particularly in homotopy theory, a model category is a category with distinguished classes of morphisms called 'weak equivalences', 'fibrations' and 'cofibrations'. These abstract from a conventional homotopy category, of topological spaces or of chain complexes...
, that is, the full subcategory consisting of those objects
 for which
for which 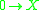 is a cofibration and
is a cofibration and 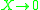 is a fibration.
is a fibration.Waldhausen and biWaldhausen categories are linked with algebraic K-theory
Algebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
. There, many interesting categories are complicial biWaldhausen categories. For example:
The category
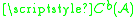 of bounded chaincomplexes on an exact category
of bounded chaincomplexes on an exact category 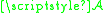
The category
 of functors
of functors 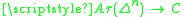 when
when  is so.
is so.And given a diagram
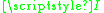 , then
, then  is a nice complicial biWaldhausen category when
is a nice complicial biWaldhausen category when 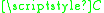 is.
is.

