Weakly compact cardinal
Encyclopedia
In mathematics
, a weakly compact cardinal is a certain kind of cardinal number
introduced by ; weakly compact cardinals are large cardinals, meaning that their existence can not be proven from the standard axioms of set theory.
Formally, a cardinal κ is defined to be weakly compact if it is uncountable and for every function f: [κ] 2 → {0, 1} there is a set of cardinality κ that is homogeneous for f. In this context, [κ] 2 means the set of 2-element subsets of κ, and a subset S of κ is homogeneous for f if and only if
either all of [S]2 maps to 0 or all of it maps to 1.
The name "weakly compact" refers to the fact that if a cardinal is weakly compact then a certain related infinitary language satisfies a version of the compactness theorem; see below.
Weakly compact cardinals are Mahlo cardinal
s, and the set of Mahlo cardinals less than a given weakly compact cardinal is stationary.
Some authors use a weaker definition of weakly compact cardinals, such as one of the conditions below with the condition of inaccessibility dropped.
A language Lκ,κ is said to satisfy the weak compactness theorem if whenever Σ is a set of sentences of cardinality at most κ and every subset with less than κ elements has a model, then Σ has a model. Strongly compact cardinal
s are defined in a similar way without the restriction on the cardinality of the set of sentences.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a weakly compact cardinal is a certain kind of cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
introduced by ; weakly compact cardinals are large cardinals, meaning that their existence can not be proven from the standard axioms of set theory.
Formally, a cardinal κ is defined to be weakly compact if it is uncountable and for every function f: [κ] 2 → {0, 1} there is a set of cardinality κ that is homogeneous for f. In this context, [κ] 2 means the set of 2-element subsets of κ, and a subset S of κ is homogeneous for f if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
either all of [S]2 maps to 0 or all of it maps to 1.
The name "weakly compact" refers to the fact that if a cardinal is weakly compact then a certain related infinitary language satisfies a version of the compactness theorem; see below.
Weakly compact cardinals are Mahlo cardinal
Mahlo cardinal
In mathematics, a Mahlo cardinal is a certain kind of large cardinal number. Mahlo cardinals were first described by . As with all large cardinals, none of these varieties of Mahlo cardinals can be proved to exist by ZFC ....
s, and the set of Mahlo cardinals less than a given weakly compact cardinal is stationary.
Some authors use a weaker definition of weakly compact cardinals, such as one of the conditions below with the condition of inaccessibility dropped.
Equivalent formulations
The following are equivalent for any uncountable cardinal κ:- κ is weakly compact.
- for every λ<κ, natural number n ≥ 2, and function f: [κ]n → λ, there is a set of cardinality κ that is homogeneous for f.
- κ is inaccessibleInaccessible cardinalIn set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...
and has the tree property, that is, every treeTree (set theory)In set theory, a tree is a partially ordered set In set theory, a tree is a partially ordered set (poset) In set theory, a tree is a partially ordered set (poset) (T, In set theory, a tree is a partially ordered set (poset) (T, ...
of height κ has either a level of size κ or a branch of size κ. - Every linear order of cardinality κ has an ascending or a descending sequence of order type κ.
- κ is
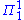-indescribableTotally indescribable cardinalIn mathematics, a Q-indescribable cardinal is a certain kind of large cardinal number that is hard to describe in some language Q. There are many different types of indescribable cardinals corresponding to different choices of languages Q...
. - κ has the extension property. In other words, for all U ⊂ Vκ there exists a transitive set X with κ ∈ X, and a subset S ⊂ X, such that (Vκ, ∈, U) is an elementary substructureElementary substructureIn model theory, a field within mathematical logic, two structures M and N of the same signature σ are called elementarily equivalent if they satisfy the same first-order σ-sentences....
of (X, ∈, S). Here, U and S are regarded as unary predicates. - For every set S of cardinality κ of subsets of κ, there is a non-trivial κ-complete filter that decides S.
- κ is κ-unfoldableUnfoldable cardinalIn mathematics, an unfoldable cardinal is a certain kind of large cardinal number.Formally, a cardinal number κ is λ-unfoldable if and only if for every transitive model M of cardinality κ of ZFC-minus-power set such that κ is in M and M contains all its sequences of length less than κ, there is a...
. - κ is inaccessible and the infinitary language Lκ,κ satisfies the weak compactness theorem.
- κ is inaccessible and the infinitary language Lκ,ω satisfies the weak compactness theorem.
A language Lκ,κ is said to satisfy the weak compactness theorem if whenever Σ is a set of sentences of cardinality at most κ and every subset with less than κ elements has a model, then Σ has a model. Strongly compact cardinal
Strongly compact cardinal
In mathematical set theory, a strongly compact cardinal is a certain kind of large cardinal number; their existence can neither be proven nor disproven from the standard axioms of set theory....
s are defined in a similar way without the restriction on the cardinality of the set of sentences.