Weight-balanced tree
Encyclopedia
A weight-balanced binary tree is a binary tree
which is balanced based on knowledge of the probabilities of searching for each individual node. Within each subtree, the node with the highest weight appears at the root. This can result in more efficient searching performance.
Construction of such a tree is similar to that of a Treap
, but node weights are chosen randomly in the latter.
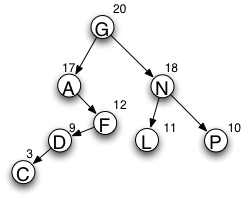
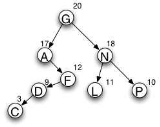
. The weight may be thought of as a probability or activity count associated with the node. In the diagram, the root is G because its weight is the greatest in the tree. The left subtree begins with A because, out of all nodes with values that come before G, A has the highest weight. Similarly, N is the highest-weighted node that comes after G.
ELOSS = depth(node A)*probability(node A) + depth(node C)*probability(node C) + ...
ELOSS = 2*0.17 + 5*0.03 + 4*0.09 + 3*0.12 + 1*0.20 + 3*0.11 + 3*0.10 + 2*0.18
ELOSS = 2.4
This is the expected number of nodes that will be examined before finding the desired node.
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
which is balanced based on knowledge of the probabilities of searching for each individual node. Within each subtree, the node with the highest weight appears at the root. This can result in more efficient searching performance.
Construction of such a tree is similar to that of a Treap
Treap
In computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys...
, but node weights are chosen randomly in the latter.

The diagram
In the diagram to the right, the letters represent node values and the numbers represent node weights. Values are used to order the tree, as in a general binary search treeBinary search tree
In computer science, a binary search tree , which may sometimes also be called an ordered or sorted binary tree, is a node-based binary tree data structurewhich has the following properties:...
. The weight may be thought of as a probability or activity count associated with the node. In the diagram, the root is G because its weight is the greatest in the tree. The left subtree begins with A because, out of all nodes with values that come before G, A has the highest weight. Similarly, N is the highest-weighted node that comes after G.
Timing analysis
A weight balanced tree gives close to optimal values for the expected length of successful search calculations. From the above example we getELOSS = depth(node A)*probability(node A) + depth(node C)*probability(node C) + ...
ELOSS = 2*0.17 + 5*0.03 + 4*0.09 + 3*0.12 + 1*0.20 + 3*0.11 + 3*0.10 + 2*0.18
ELOSS = 2.4
This is the expected number of nodes that will be examined before finding the desired node.
See also
- Binary treeBinary treeIn computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
- AVL treeAVL treeIn computer science, an AVL tree is a self-balancing binary search tree, and it was the first such data structure to be invented. In an AVL tree, the heights of the two child subtrees of any node differ by at most one. Lookup, insertion, and deletion all take O time in both the average and worst...
- B-treeB-treeIn computer science, a B-tree is a tree data structure that keeps data sorted and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree is a generalization of a binary search tree in that a node can have more than two children...
- Binary space partitioningBinary space partitioningIn computer science, binary space partitioning is a method for recursively subdividing a space into convex sets by hyperplanes. This subdivision gives rise to a representation of the scene by means of a tree data structure known as a BSP tree.Originally, this approach was proposed in 3D computer...
- Red-black treeRed-black treeA red–black tree is a type of self-balancing binary search tree, a data structure used in computer science, typically to implement associative arrays. The original structure was invented in 1972 by Rudolf Bayer and named "symmetric binary B-tree," but acquired its modern name in a paper in 1978 by...
- TreapTreapIn computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys...

