
Weighted geometric mean
Encyclopedia
In statistics
, given a set of data,

and corresponding weights
,

the weighted geometric mean is calculated as
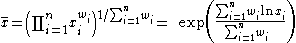
Note that if all the weights are equal, the weighted geometric mean is the same as the geometric mean
.
Weighted versions of other means can also be calculated. Probably the best known weighted mean is the weighted arithmetic mean, usually simply called the weighted mean
. Another example of a weighted mean is the weighted harmonic mean.
The second form above illustrates that the logarithm
of the geometric mean is the weighted arithmetic mean of the logarithms of the individual values.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, given a set of data,

and corresponding weights
Weight function
A weight function is a mathematical device used when performing a sum, integral, or average in order to give some elements more "weight" or influence on the result than other elements in the same set. They occur frequently in statistics and analysis, and are closely related to the concept of a...
,

the weighted geometric mean is calculated as
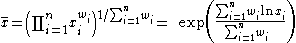
Note that if all the weights are equal, the weighted geometric mean is the same as the geometric mean
Geometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
.
Weighted versions of other means can also be calculated. Probably the best known weighted mean is the weighted arithmetic mean, usually simply called the weighted mean
Weighted mean
The weighted mean is similar to an arithmetic mean , where instead of each of the data points contributing equally to the final average, some data points contribute more than others...
. Another example of a weighted mean is the weighted harmonic mean.
The second form above illustrates that the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of the geometric mean is the weighted arithmetic mean of the logarithms of the individual values.

